题目内容
12.已知抛物线y2=2x的准线l与x轴的交点为K,点A、B在抛物线上,若$\overrightarrow{AB}$=3$\overrightarrow{KA}$,则AB的斜率为( )| A. | ±$\frac{4}{5}$ | B. | ±$\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{4}$ |
分析 求出抛物线的准线方程,可得K的坐标,可设A($\frac{{m}^{2}}{2}$,m),B($\frac{{n}^{2}}{2}$,n),运用向量共线的坐标表示,解方程可得m,n,再由直线的斜率公式,计算即可得到所求值.
解答 解:抛物线y2=2x的准线l为x=-$\frac{1}{2}$,
即有K(-$\frac{1}{2}$,0),
由A,B在抛物线上,可设A($\frac{{m}^{2}}{2}$,m),B($\frac{{n}^{2}}{2}$,n),
由$\overrightarrow{AB}$=3$\overrightarrow{KA}$,可得$\frac{{n}^{2}}{2}$-$\frac{{m}^{2}}{2}$=3($\frac{{m}^{2}}{2}$+$\frac{1}{2}$),
且n-m=3(m-0),
解得m=$\frac{1}{2}$,n=2或m=-$\frac{1}{2}$,n=-2,
即有直线AB的斜率为k=$\frac{n-m}{\frac{{n}^{2}}{2}-\frac{{m}^{2}}{2}}$=$\frac{2}{m+n}$=$\frac{2}{\frac{1}{2}+2}$=$\frac{4}{5}$
或$\frac{2}{-\frac{1}{2}-2}$=-$\frac{4}{5}$.
故选:A.
点评 本题考查抛物线的方程及运用,考查向量共线的坐标表示,以及直线的斜率公式的运用,考查运算能力,属于中档题.

练习册系列答案
相关题目
3.在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥平面ABCD,AB=PD=a,E为侧棱PC的中点,又作DF⊥PB交PB于点F,则PB与平面EFD所成角为( )
| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
20.下列各组中的两个函数是相等函数的是( )
| A. | y=x与y=$\frac{{x}^{2}}{x}$ | B. | y=($\sqrt{x}$)2-1与y=|x|-1 | C. | y=x2与y=$\root{3}{{x}^{6}}$ | D. | y=$\root{3}{{x}^{3}}与y=\sqrt{{x}^{2}}$ |
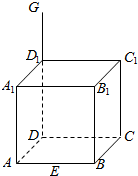 如图,G是正方体ABCD-A1B1C1D1的棱DD1延长线上的一点,E、F是棱AB、BC的中点,试分别画出过下列各点、直线的平面与正方体表面的交线.
如图,G是正方体ABCD-A1B1C1D1的棱DD1延长线上的一点,E、F是棱AB、BC的中点,试分别画出过下列各点、直线的平面与正方体表面的交线.