题目内容
已知函数f(x)=cos2x+2sinxcosx-sin2x
(Ⅰ)求f(
)的值;
(Ⅱ)求函数f(x)的单调增区间与最大值.
(Ⅰ)求f(
| π |
| 4 |
(Ⅱ)求函数f(x)的单调增区间与最大值.
考点:三角函数中的恒等变换应用,正弦函数的图象
专题:三角函数的图像与性质
分析:(Ⅰ)把x=
代入函数解析式求得答案.
(Ⅱ)利用二倍角公式和两角和公式对函数解析式化简,利用三角函数的性质求得单调区间和最大值.
| π |
| 4 |
(Ⅱ)利用二倍角公式和两角和公式对函数解析式化简,利用三角函数的性质求得单调区间和最大值.
解答:
解:(Ⅰ)∵f(x)=cos2x+2sinxcosx-sin2x
∴f(
)=(
)2+2-
×
-(
)2=1.
(Ⅱ)∵f(x)=cos2x+2sinxcosx-sin2x=sin2x+cos2x=
sin(2x+
),
∴当-
+2kπ≤2x+
≤
+2kπ,k∈Z,即-
+kπ≤x≤
+kπ,k∈Z,函数单调增,
∴函数f(x)的单调增区间是[-
+kπ,
+kπ](k∈Z),
当2x+
=
+2kπ,即x=
+kπ(k∈Z)时,f(x)有最大值为
∴f(
| π |
| 4 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
(Ⅱ)∵f(x)=cos2x+2sinxcosx-sin2x=sin2x+cos2x=
| 2 |
| π |
| 4 |
∴当-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| 3π |
| 8 |
| π |
| 8 |
∴函数f(x)的单调增区间是[-
| 3π |
| 8 |
| π |
| 8 |
当2x+
| π |
| 4 |
| π |
| 2 |
| π |
| 8 |
| 2 |
点评:本题主要考查了三角函数恒等变换的应用,三角函数图象与性质.考查了学生对基础知识的掌握.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
sin61°cos31°-cos61°sin31°=( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
 如图,在平面直角坐标系中,锐角α,β的终边分别与单位圆交于A、B两点.
如图,在平面直角坐标系中,锐角α,β的终边分别与单位圆交于A、B两点.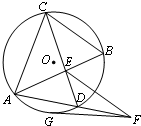 如图,E是圆O内两弦AB和CD的交点,过AD延长线上一点F作圆O的切线FG,G为切点,已知EF=FG.求证:
如图,E是圆O内两弦AB和CD的交点,过AD延长线上一点F作圆O的切线FG,G为切点,已知EF=FG.求证: