题目内容
已知tanα=
,cos(α+β)=-
,且α∈(0,
),β∈(-
,
),
(1)求
的值;
(2)求β的值.
| 3 |
| 4 |
7
| ||
| 10 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
(1)求
2cos2
| ||||
|
(2)求β的值.
考点:三角函数中的恒等变换应用
专题:三角函数的图像与性质
分析:(1)首先,根据二倍角公式化简,然后,分子分母同除以cosα,从而转化成用tanα表示的式子,然后,代入求值即可;
(2)先求解sin(α+β)的值,然后,求tan(α+β)的值,结合tanβ=tan[(α+β)-α],从而,确定待求的β的值.
(2)先求解sin(α+β)的值,然后,求tan(α+β)的值,结合tanβ=tan[(α+β)-α],从而,确定待求的β的值.
解答:
解:(1)
=
=
=
=
,
∴
的值为
;
(2)∵α∈(0,
),β∈(-
,
),
∴(α+β)∈(-
,π),
又∵cos(α+β)=-
<0,
∴(α+β)∈(
,π),
∴sin(α+β)=
=
=
,
∴tan(α+β)=
=
=-
,
∵tanβ=tan[(α+β)-α]
=
=
=-
,
∴β=-arctan
.
2cos2
| ||||
|
=
| cosα-sinα |
| sinα+cosα |
=
| 1-tanα |
| 1+tanα |
=
1-
| ||
1+
|
=
| 1 |
| 7 |
∴
2cos2
| ||||
|
| 1 |
| 7 |
(2)∵α∈(0,
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
∴(α+β)∈(-
| π |
| 2 |
又∵cos(α+β)=-
7
| ||
| 10 |
∴(α+β)∈(
| π |
| 2 |
∴sin(α+β)=
| 1-cos2(α+β) |
=
1-(-
|
| ||
| 10 |
∴tan(α+β)=
| sin(α+β) |
| cos(α+β) |
=
| ||||
|
| 1 |
| 7 |
∵tanβ=tan[(α+β)-α]
=
| tan(α+β)-tanα |
| 1+tan(α+β)tanα |
=
-
| ||||
1-(-
|
=-
| 25 |
| 31 |
∴β=-arctan
| 25 |
| 31 |
点评:本题综合考查了两角和与差的正切公式,角的灵活拆分等知识,属于中档题.

练习册系列答案
相关题目
 如图,在平面直角坐标系中,锐角α,β的终边分别与单位圆交于A、B两点.
如图,在平面直角坐标系中,锐角α,β的终边分别与单位圆交于A、B两点.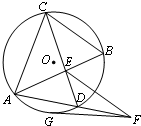 如图,E是圆O内两弦AB和CD的交点,过AD延长线上一点F作圆O的切线FG,G为切点,已知EF=FG.求证:
如图,E是圆O内两弦AB和CD的交点,过AD延长线上一点F作圆O的切线FG,G为切点,已知EF=FG.求证: