题目内容
1．
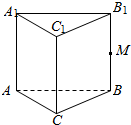如图所示，在三棱柱ABC-A1B1C1中，M是BB1的中点，化简下列各式，并在图中标出化简得到的向量：（1）$\overrightarrow{CB}$+$\overrightarrow{B{A}_{1}}$；
（2）$\overrightarrow{AC}$+$\overrightarrow{CB}$+$\frac{1}{2}$$\overrightarrow{A{A}_{1}}$；
（3）$\overrightarrow{A{A}_{1}}$-$\overrightarrow{AC}$-$\overrightarrow{CB}$．
分析 利用空间向量的加减法的运算法则和几何意义化简．
解答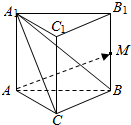 
解：（1）$\overrightarrow{CB}$+$\overrightarrow{B{A}_{1}}$=$\overrightarrow{C{A}_{1}}$，
（2）$\overrightarrow{AC}$+$\overrightarrow{CB}$+$\frac{1}{2}$$\overrightarrow{A{A}_{1}}$=$\overrightarrow{AB}+\frac{1}{2}\overrightarrow{A{A}_{1}}$=$\overrightarrow{AM}$；
（3）$\overrightarrow{A{A}_{1}}$-$\overrightarrow{AC}$-$\overrightarrow{CB}$=$\overrightarrow{C{A}_{1}}$-$\overrightarrow{CB}$=$\overrightarrow{B{A}_{1}}$．
点评 本题考查了空间向量线性运算及其几何意义，是基础题．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
12．已知定义在R上的函数f（x）满足当∈[2k-1，2k+1）（k∈Z）时f（x）=（x-2k）2，若y=f（x）与g（x）=logax图象上关于y轴对称的点有3对，则a的取值范围是（ ）
| A． | （0，2） | B． | （1，3） | C． | （2，4） | D． | （3，5） |
9．函数f（x）=|x2-a2|（α＞0），动点P（m，n）满足f（m）=f（n），且m＜n＜0，若动点P（m，n）的轨迹直线x+y+1=0没有公共点，则实数a的取值范围是（ ）
| A． | （0，$\frac{1}{2}$） | B． | （$\frac{1}{2}$，$\frac{\sqrt{2}}{2}$） | C． | （$\frac{\sqrt{2}}{2}$，+∞） | D． | （0，$\frac{1}{2}$]∪[$\frac{\sqrt{2}}{2}$，+∞） |
16．下列函数中在（$\frac{π}{4}$，$\frac{3}{4}$π）上为减函数的是（ ）
| A． | y=-tanx | B． | y=cos（2x-$\frac{π}{2}$） | C． | y=sin2x+cos2x | D． | y=2cos2x-1 |
6．已知△ABC中角A，B，C的对边分别是a，b，c，满足c=a•cos（A+C），则tanC的最大值为（ ）
| A． | $\sqrt{2}$ | B． | $\frac{\sqrt{2}}{4}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{3}}{3}$ |
6．用简单随机抽样的方法从含有10个个体的总体中，抽取一个容量为3的样本，其中某一个体a“第一次被抽到”的可能性，“第二次被抽到”的可能性分别是（ ）
| A． | $\frac{1}{10}$，$\frac{1}{10}$ | B． | $\frac{3}{10}$，$\frac{1}{5}$ | C． | $\frac{1}{5}$，$\frac{3}{10}$ | D． | $\frac{3}{10}$，$\frac{3}{10}$ |