题目内容
9.函数f(x)=|x2-a2|(α>0),动点P(m,n)满足f(m)=f(n),且m<n<0,若动点P(m,n)的轨迹直线x+y+1=0没有公共点,则实数a的取值范围是( )| A. | (0,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,$\frac{\sqrt{2}}{2}$) | C. | ($\frac{\sqrt{2}}{2}$,+∞) | D. | (0,$\frac{1}{2}$]∪[$\frac{\sqrt{2}}{2}$,+∞) |
分析 由题意画出图形,结合动点P(m,n)满足f(m)=f(n),且m<n<0,得到P的轨迹m2+n2=2a2($-\sqrt{2}a<m<-a$,-a<n<0).再作出P的轨迹与直线x+y+1=0的图象,数形结合求出使P的轨迹与直线x+y+1=0有交点的a的范围,利用补集思想得答案.
解答 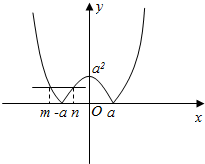 解:作出函数f(x)=|x2-a2|(a>0)的图象如图:
解:作出函数f(x)=|x2-a2|(a>0)的图象如图:
动点P(m,n)满足f(m)=f(n),且m<n<0,
则-a<n<0,
由x2-a2=a2,解得x=$±\sqrt{2}a$,∴$-\sqrt{2}a<m<-a$.
由f(m)=f(n),得|m2-a2|=|n2-a2|,
即m2-a2=-n2+a2,∴m2+n2=2a2.
∴动点P(m,n)的轨迹为m2+n2=2a2($-\sqrt{2}a<m<-a$,-a<n<0).
作出P的轨迹与直线x+y+1=0的图象如图: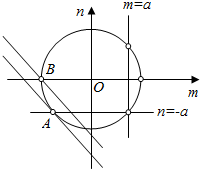
P的轨迹为圆m2+n2=2a2上不含端点A,B的劣弧,
要使P的轨迹与直线x+y+1=0有交点,则-2a<-1<-$\sqrt{2}$a,解得:$\frac{1}{2}<a<\frac{\sqrt{2}}{2}$.
∴使动点P(m,n)的轨迹与直线x+y+1=0没有公共点的实数a的取值范围是(0,$\frac{1}{2}$]∪[$\frac{\sqrt{2}}{2}$,+∞).
故选:D.
点评 本题考查轨迹方程,考查数形结合的解题思想方法和数学转化思想方法,关键是对题意的理解,有一定难度.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
17.若函数f(x)满足f(x+1)=x2-x+2,则f(-1)=( )
| A. | 8 | B. | 5 | C. | 4 | D. | 3 |
4.已知函数f(x)=(2a-1)x+3在R上为减函数,则有( )
| A. | a>$\frac{1}{2}$ | B. | a<$\frac{1}{2}$ | C. | a≥$\frac{1}{2}$ | D. | a≤$\frac{1}{2}$ |
14.下列说法中正确的是( )
| A. | 向量$\overrightarrow{a}$与非零向量$\overrightarrow{b}$共线,$\overrightarrow{b}$与$\overrightarrow{c}$共线,则$\overrightarrow{a}$与$\overrightarrow{c}$共线 | |
| B. | 任意两个相等向量不一定是共线向量 | |
| C. | 任意两个共线向量相等 | |
| D. | 若向量$\overrightarrow{a}$与$\overrightarrow{b}$共线,则$\overrightarrow{a}$=λ$\overrightarrow{b}$(λ>0) |
18.1~100中所有奇数的和为( )
| A. | 99 | B. | 1250 | C. | 2500 | D. | 2525 |
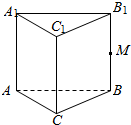 如图所示,在三棱柱ABC-A1B1C1中,M是BB1的中点,化简下列各式,并在图中标出化简得到的向量:
如图所示,在三棱柱ABC-A1B1C1中,M是BB1的中点,化简下列各式,并在图中标出化简得到的向量: