题目内容
6.用简单随机抽样的方法从含有10个个体的总体中,抽取一个容量为3的样本,其中某一个体a“第一次被抽到”的可能性,“第二次被抽到”的可能性分别是( )| A. | $\frac{1}{10}$,$\frac{1}{10}$ | B. | $\frac{3}{10}$,$\frac{1}{5}$ | C. | $\frac{1}{5}$,$\frac{3}{10}$ | D. | $\frac{3}{10}$,$\frac{3}{10}$ |
分析 在抽样过程中,个体a每一次被抽中的概率是相等的,结合已知中的总体容量,可得答案.
解答 解:在抽样过程中,个体a每一次被抽中的概率是相等的,
∵总体容量为10,
故个体a“第一次被抽到”的可能性,“第二次被抽到”的可能性均为$\frac{1}{10}$,
故选:A
点评 本题考查的知识点是简单随机抽样,正确理解简单随机抽样中的等可能性,是解答的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
17.函数f(x)=ln(x2-2x-3)的定义域为( )
| A. | (-1,3) | B. | (-∞,-1)∪(3,+∞) | C. | [-3,1] | D. | (-∞,-1]∪[3,+∞) |
1.已知椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{m}$=1的离心率e=$\frac{1}{2}$,则m的值为( )
| A. | 3 | B. | 1 | C. | 16或1 | D. | $\frac{16}{3}$或3 |
11.“x-3=0”是“(x-3)(x+4)=0”的( )条件.
| A. | 充要 | B. | 充分不必要 | ||
| C. | 必要不充分 | D. | 既不充分又不必要 |
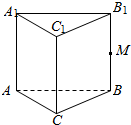 如图所示,在三棱柱ABC-A1B1C1中,M是BB1的中点,化简下列各式,并在图中标出化简得到的向量:
如图所示,在三棱柱ABC-A1B1C1中,M是BB1的中点,化简下列各式,并在图中标出化简得到的向量: