题目内容
12.已知定义在R上的函数f(x)满足当∈[2k-1,2k+1)(k∈Z)时f(x)=(x-2k)2,若y=f(x)与g(x)=logax图象上关于y轴对称的点有3对,则a的取值范围是( )| A. | (0,2) | B. | (1,3) | C. | (2,4) | D. | (3,5) |
分析 题目中:“函数f(x)=(x-2k)2,x∈[2k-1,2k+1],k∈Z,”的图象是一段一段的抛物线段,如图,y=f(x)与g(x)=logax图象上关于y轴对称的点有3对,则两个函数f(x)和g(x)的交点个数是三个.
解答  解:分别画出简图,如下:
解:分别画出简图,如下:
y=f(x)与g(x)=logax图象上关于y轴对称的点有3对,则两个函数f(x)和g(x)的交点个数是三个,
∴a>1,loga3<1且loga5>1,
∴3<a<5.
故选:D.
点评 本题主要考查图象法求函数的零点,数形结合是重要的数学思想,以形助数,直观简捷,从而利用函数图象可以进一步发现函数性质.

练习册系列答案
相关题目
7.已知点P(2,2)在直线l:Ax+By+C=0上,则方程Bx-Ay+4A+C=0是( )
| A. | 不过点P且与l垂直的直线 | B. | 不过点P且与l平行的直线 | ||
| C. | 过点P且与l垂直的直线 | D. | 过点P且与l平行的直线 |
17.若函数f(x)满足f(x+1)=x2-x+2,则f(-1)=( )
| A. | 8 | B. | 5 | C. | 4 | D. | 3 |
4.已知函数f(x)=(2a-1)x+3在R上为减函数,则有( )
| A. | a>$\frac{1}{2}$ | B. | a<$\frac{1}{2}$ | C. | a≥$\frac{1}{2}$ | D. | a≤$\frac{1}{2}$ |
17.函数f(x)=ln(x2-2x-3)的定义域为( )
| A. | (-1,3) | B. | (-∞,-1)∪(3,+∞) | C. | [-3,1] | D. | (-∞,-1]∪[3,+∞) |
 如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.
如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.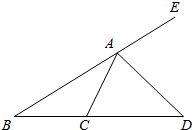 如图,AD是△ABC的外角∠EAC的平分线,那么$\frac{AB}{AC}$=$\frac{BD}{DC}$成立吗?
如图,AD是△ABC的外角∠EAC的平分线,那么$\frac{AB}{AC}$=$\frac{BD}{DC}$成立吗?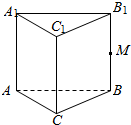 如图所示,在三棱柱ABC-A1B1C1中,M是BB1的中点,化简下列各式,并在图中标出化简得到的向量:
如图所示,在三棱柱ABC-A1B1C1中,M是BB1的中点,化简下列各式,并在图中标出化简得到的向量: