题目内容
11.数列{an}为等差数列,且a1=8,a4=2(1)求数列{an}的通项公式;
(2)设Sn=|a1|+|a2|+…+|an|,求Sn.
分析 (1)利用公差d=$\frac{{a}_{4}-{a}_{1}}{3-1}$计算即得结论;
(2)通过(1)分1≤n≤5、n>5两种情况讨论即可.
解答 解:(1)∵a1=8,a4=2,
∴公差d=$\frac{{a}_{4}-{a}_{1}}{3-1}$=$\frac{2-8}{3}$=-2,
∴数列{an}的通项公式an=a1+(n-1)d=8-2(n-1)=-2n+10;
(2)由(1)可知当n=5时an=0,当1≤n<5时an>0,当n>5时an<0,
且数列{an}的前n项和Tn=$\frac{n(8-2n+10)}{2}$=-n2+9n,
∴当1≤n≤5时,Sn=Tn=-n2+9n;
当n>5时,Sn=-Tn+2T5=n2-9n+2(-25+45)=n2-9n+40;
综上所述,Sn=$\left\{\begin{array}{l}{-{n}^{2}+9n,}&{1≤n≤5}\\{{n}^{2}-9n+40,}&{n>5}\end{array}\right.$.
点评 本题考查数列的通项及前n项和,考查分类讨论的思想,注意解题方法的积累,属于中档题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
1.在{an}为等比数列,a1=12,a2=24,则a3=( )
| A. | 36 | B. | 48 | C. | 60 | D. | 72 |
6.已知$\overrightarrow{AB}$=(5,-3),点A(3,1),则点B的坐标为( )
| A. | (2,2) | B. | (-2,-2) | C. | (8,-2) | D. | (4,8) |
 如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.
如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.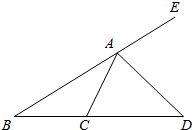 如图,AD是△ABC的外角∠EAC的平分线,那么$\frac{AB}{AC}$=$\frac{BD}{DC}$成立吗?
如图,AD是△ABC的外角∠EAC的平分线,那么$\frac{AB}{AC}$=$\frac{BD}{DC}$成立吗?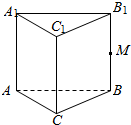 如图所示,在三棱柱ABC-A1B1C1中,M是BB1的中点,化简下列各式,并在图中标出化简得到的向量:
如图所示,在三棱柱ABC-A1B1C1中,M是BB1的中点,化简下列各式,并在图中标出化简得到的向量: