题目内容
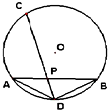如图，AB，CD是⊙O的两条弦，它们相交于P，连结AD，BD．已知AD=BD=4，PC=6，那么CD的长为考点：与圆有关的比例线段
专题：推理和证明,立体几何
分析：根据AD=BD=4，
=
，∠DAB=∠DBA，确定出∠DAB=∠ACD，∠CDA=∠ADP，判断△APD∽△CAD，运用对应边成比例即可判断求解．
 |
| AD |
|
| BD |
解答：
解：
连接AC，DP=x，CD=6+x
∵AD=BD=4，
∴
=
，∠DAB=∠DBA，
∴∠ACD=∠DAB，
即∠DAB=∠ACD，
∵∠CDA=∠ADP，
∴△APD∽△CAD，
对应边成比例，
∴
=
，
=
，
化简计算得出：x2+6x-16=0，求解得出：x=2，x=-8（舍去）
∴x+6=2+6=8，
故答案为：8
连接AC，DP=x，CD=6+x
∵AD=BD=4，
∴
|
| AD |
|
| BD |
∴∠ACD=∠DAB，
即∠DAB=∠ACD，
∵∠CDA=∠ADP，
∴△APD∽△CAD，
对应边成比例，
∴
| AD |
| CD |
| DP |
| AD |
| 4 |
| 6+x |
| x |
| 4 |
化简计算得出：x2+6x-16=0，求解得出：x=2，x=-8（舍去）
∴x+6=2+6=8，
故答案为：8
点评：本题考查了圆周角，弦长问题，判断有关的角相等问题，得出相似三角形，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
设a=log23，b=log2
，c=（
）1.2，则它们的大小关系是（ ）
| 1 |
| 3 |
| 1 |
| 2 |
| A、c＜a＜b |
| B、b＜c＜a |
| C、b＜a＜c |
| D、c＜b＜a |