题目内容
已知梯形ABCD中，AD=1，AB=2，∠DAB=
，DC∥AB，若
=λ
，则当
•
=-
时，λ= ．
| π |
| 3 |
| DE |
| DC |
| AE |
| BD |
| 3 |
| 4 |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：由题意可得
=
+
=
+λ
；
=
-
；从而得到
2-
•
+λ
•
-λ
•
=-
；从而化简求λ的值．
| AE |
| AD |
| DE |
| AD |
| DC |
| BD |
| AD |
| AB |
| AD |
| AD |
| AB |
| DC |
| AD |
| DC |
| AB |
| 3 |
| 4 |
解答：
解：
=
+
=
+λ
；
=
-
；
∵
•
=-
；
∴（
+λ
）•（
-
）=-
；
∴
2-
•
+λ
•
-λ
•
=-
；
即1-1×2×cos
+λ|
|cos
-λ|
|•2=-
；
故-
λ|
|=-
；
故λ=
．
故答案为：
．
| AE |
| AD |
| DE |
| AD |
| DC |
| BD |
| AD |
| AB |
∵
| AE |
| BD |
| 3 |
| 4 |
∴（
| AD |
| DC |
| AD |
| AB |
| 3 |
| 4 |
∴
| AD |
| AD |
| AB |
| DC |
| AD |
| DC |
| AB |
| 3 |
| 4 |
即1-1×2×cos
| π |
| 3 |
| DC |
| π |
| 3 |
| DC |
| 3 |
| 4 |
故-
| 3 |
| 2 |
| DC |
| 3 |
| 4 |
故λ=
| 1 | ||
2|
|
故答案为：
| 1 | ||
2|
|
点评：本题考查了平面向量的线性运算及数量积的运用，属于中档题．
练习册系列答案
相关题目
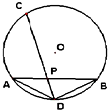如图，AB，CD是⊙O的两条弦，它们相交于P，连结AD，BD．已知AD=BD=4，PC=6，那么CD的长为
已知y=f（x）是定义在（-∞，0）∪（0，+∞）上的奇函数，当x＞0时，f（x）=log2x，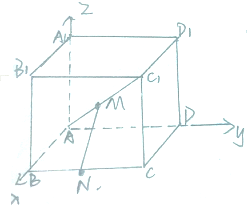
在棱长为1的正方体ABCD-A1B1C1D1中，动点M在线段AC1上，动点N在线段BC上，建立空间直角坐标系（如图所示），求线段MN长度最小值，以及此时点M，N的坐标．