题目内容

设a=log23，b=log2
1
3
，c=（
1
2
）1.2，则它们的大小关系是（　　）
A、c＜a＜b
B、b＜c＜a
C、b＜a＜c
D、c＜b＜a
考点：对数值大小的比较
专题：函数的性质及应用
分析：利用对数函数、指数函数的单调性求解．
解答： 解：∵a=log23＞log22=1，
b=log2
1
3
＜log21=0，
0＜c=（
1
2
）1.2＜（
1
2
）0=1．
∴b＜c＜a．
故选：B．
点评：本题考查三个数的大小的比较，是基础题，解题时要认真审题，注意函数性质的合理运用．
练习册系列答案
相关题目
直角坐标的坐标原点与极坐标的极点重合，x轴正半轴为极轴，长度单位相同．若直线l方程
x=t-1
y=2t-3
（t为参数），圆C方程为ρ=2COSθ，ρ与⊙C相交于A、B两点．
（Ⅰ）写出直线l的极坐标方程（不必化简）；
（Ⅱ）求弦长|AB|．
已知
a
=（
3
sinωx，-cosωx），
b
=（cosωx，cosωx），ω＞0，函数f(x)=
a
•
b
，且f（x）的图象相邻两条对称轴间的距离为
π
2
．
（Ⅰ）求函数f（x）的最小正周期和单调增区间；
（Ⅱ）已知△ABC的内角A，B，C所对的边分别为a，b，c，若a=
7
，b=2，且f（
A
2
）=
1
2
，求△ABC的面积．
若复数z满足（3+4i）z=4-3i，则z的虚部为（　　）
A、1B、iC、-1D、-i
设函数f（x）=4cos2x（cos2x-1）+3-4cos2x．
（1）求使f（x）＞0的x取值范围；
（2）求x为何值时f（x）取得最大值和最小值．
已知α，β为锐角，
sinα
cosβ
+
sinβ
cosα
=2，则有（　　）
A、α+β＞
π
2
B、α+β=
π
2
C、α+β＜
π
2
D、α+β=
π
4
已知角a∈（0，4π），且a与-
2
5
π的终边相同，则a=
 
．
2(1+i3)
(1+i)2
=
 
．
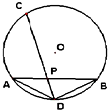 如图，AB，CD是⊙O的两条弦，它们相交于P，连结AD，BD．已知AD=BD=4，PC=6，那么CD的长为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网