题目内容
已知sin(3π-α)=
cos(
π+β),
sin(
-α)=-
sin(
+β),且0<α<π,0<β<π,求sinα,cosβ.
| 2 |
| 3 |
| 2 |
| 3 |
| π |
| 2 |
| 2 |
| 3π |
| 2 |
考点:运用诱导公式化简求值,三角函数的化简求值
专题:三角函数的求值
分析:利用诱导公式可得sinα=
sinβ,
cosα=
cosβ,利用平方关系可得sin2α+3cos2α=2(sin2β+cos2β)=2,cosα=±
.再利用0<α<π,可得α=
或
.即可解出sinα,cosβ.
| 2 |
| 3 |
| 2 |
| ||
| 2 |
| π |
| 4 |
| 3π |
| 4 |
解答:
解:∵sin(3π-α)=
cos(
π+β),
sin(
-α)=-
sin(
+β),
∴sinα=
sinβ,
cosα=
cosβ,
∴sin2α+3cos2α=2(sin2β+cos2β)=2,
化为cos2α=
,∴cosα=±
.
∵0<α<π,∴α=
或
.
当α=
时,∵sinα=
sinβ,
cosα=
cosβ,0<β<π,
∴sinα=
,cosβ=
.
当α=
时,∵sinα=
sinβ,
cosα=
cosβ,0<β<π,
∴sinα=
,cosβ=-
.
| 2 |
| 3 |
| 2 |
| 3 |
| π |
| 2 |
| 2 |
| 3π |
| 2 |
∴sinα=
| 2 |
| 3 |
| 2 |
∴sin2α+3cos2α=2(sin2β+cos2β)=2,
化为cos2α=
| 1 |
| 2 |
| ||
| 2 |
∵0<α<π,∴α=
| π |
| 4 |
| 3π |
| 4 |
当α=
| π |
| 4 |
| 2 |
| 3 |
| 2 |
∴sinα=
| ||
| 2 |
| ||
| 2 |
当α=
| 3π |
| 4 |
| 2 |
| 3 |
| 2 |
∴sinα=
| ||
| 2 |
| ||
| 2 |
点评:本题考查了诱导公式、同角三角函数基本关系式、三角函数值所在象限的符号,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
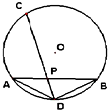 如图,AB,CD是⊙O的两条弦,它们相交于P,连结AD,BD.已知AD=BD=4,PC=6,那么CD的长为
如图,AB,CD是⊙O的两条弦,它们相交于P,连结AD,BD.已知AD=BD=4,PC=6,那么CD的长为
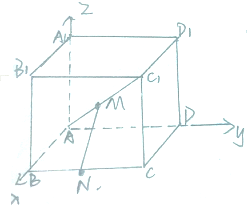 在棱长为1的正方体ABCD-A1B1C1D1中,动点M在线段AC1上,动点N在线段BC上,建立空间直角坐标系(如图所示),求线段MN长度最小值,以及此时点M,N的坐标.
在棱长为1的正方体ABCD-A1B1C1D1中,动点M在线段AC1上,动点N在线段BC上,建立空间直角坐标系(如图所示),求线段MN长度最小值,以及此时点M,N的坐标.