题目内容
判断函数y=x3+x的单调性和奇偶性，并证明你的结论．
考点：函数奇偶性的判断,函数单调性的判断与证明
专题：函数的性质及应用
分析：易得函数y=x3+x为R上的单调递增函数和奇函数，求导数和奇函数的定义可证．
解答：
解：函数y=x3+x为R上的单调递增函数和奇函数，下面证明：
求导数可得y=3x2+1＞0，∴y=x3+x为R上的单调递增函数，
令f（x）=x3+x，则f（-x）=（-x）3+（-x）=-x3-x=-f（x），
∴y=x3+x为R上的奇函数
求导数可得y=3x2+1＞0，∴y=x3+x为R上的单调递增函数，
令f（x）=x3+x，则f（-x）=（-x）3+（-x）=-x3-x=-f（x），
∴y=x3+x为R上的奇函数
点评：本题考查函数的单调性和奇偶性，属基础题．
练习册系列答案
相关题目
已知α，β为锐角，
+
=2，则有（ ）
| sinα |
| cosβ |
| sinβ |
| cosα |
A、α+β＞
| ||
B、α+β=
| ||
C、α+β＜
| ||
D、α+β=
|
若（a-3）-3＜（1+2a）-3，则实数a的取值范围是（ ）
| A、（-4，+∞） | ||
B、{a|a＞-4，a≠3且a≠-
| ||
| C、（-∞，-4） | ||
D、（-∞，-4）∪（-
|
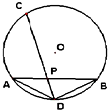如图，AB，CD是⊙O的两条弦，它们相交于P，连结AD，BD．已知AD=BD=4，PC=6，那么CD的长为
已知y=f（x）是定义在（-∞，0）∪（0，+∞）上的奇函数，当x＞0时，f（x）=log2x，