题目内容
下列有关命题的说法正确的是 .
①命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1”;
②已知x>0时,(x-1)f′(x)<0,若△ABC是锐角三角形,则f(sinA)>f(cosB);
③命题“若x=y,则sinx=siny”的逆否命题为真命题;
④命题“?x∈R使得x2+x+1<0”的否定是:“?x∈R均有x2+x+1>0”.
①命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1”;
②已知x>0时,(x-1)f′(x)<0,若△ABC是锐角三角形,则f(sinA)>f(cosB);
③命题“若x=y,则sinx=siny”的逆否命题为真命题;
④命题“?x∈R使得x2+x+1<0”的否定是:“?x∈R均有x2+x+1>0”.
考点:命题的真假判断与应用
专题:综合题,简易逻辑
分析:①写出命题“若x2=1,则x=1”的否命题即可;
②根据题意,f(x)在(0,1)上是增函数,由此判断锐角△ABC中,f(sinA)>f(cosB);
③判断命题“若x=y,则sinx=siny”的真假性,得出它的逆否命题的真假性;
④写出命题“?x∈R使得x2+x+1<0”的否定命题是什么.
②根据题意,f(x)在(0,1)上是增函数,由此判断锐角△ABC中,f(sinA)>f(cosB);
③判断命题“若x=y,则sinx=siny”的真假性,得出它的逆否命题的真假性;
④写出命题“?x∈R使得x2+x+1<0”的否定命题是什么.
解答:
解:对于①,命题“若x2=1,则x=1”的否命题为:“若x2≠1,则x≠1”,∴①错误;
对于②,x>0时,(x-1)f′(x)<0,∴f(x)在(0,1)上是增函数,
当△ABC是锐角三角形时,A+B>
,∴A>
-B,∴sinA>sin(
-B)=cosB,
∴f(sinA)>f(cosB),②正确;
对于③,命题“若x=y,则sinx=siny”是真命题,∴它的逆否命题为真命题,③正确;
对于④,命题“?x∈R使得x2+x+1<0”的否定是:“?x∈R均有x2+x+1≥0”,∴④错误.
综上,以上正确的命题是②③.
故答案为:②③.
对于②,x>0时,(x-1)f′(x)<0,∴f(x)在(0,1)上是增函数,
当△ABC是锐角三角形时,A+B>
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
∴f(sinA)>f(cosB),②正确;
对于③,命题“若x=y,则sinx=siny”是真命题,∴它的逆否命题为真命题,③正确;
对于④,命题“?x∈R使得x2+x+1<0”的否定是:“?x∈R均有x2+x+1≥0”,∴④错误.
综上,以上正确的命题是②③.
故答案为:②③.
点评:本题考查了否命题与命题的否定问题,利用导数判断函数的增减性问题,命题与逆否命题的真假性问题,是综合性题目.

练习册系列答案
相关题目
若复数z满足(3+4i)z=4-3i,则z的虚部为( )
| A、1 | B、i | C、-1 | D、-i |
下列说法正确的个数为( )
①“x>y”是“lgx>lgy”的充要条件;
②“a>b”是“ac2>bc2”的必要不充分条件;
③“k=
”是“直线y=kx+2与圆x2+y2=1相切”的充分不必要条件;
④“α>β”是“sinα>sinβ”既不充分又不必要条件.
①“x>y”是“lgx>lgy”的充要条件;
②“a>b”是“ac2>bc2”的必要不充分条件;
③“k=
| 3 |
④“α>β”是“sinα>sinβ”既不充分又不必要条件.
| A、3 个 |
| B、4 个 |
| C、1 个 |
| D、2个 |
若(a-3)-3<(1+2a)-3,则实数a的取值范围是( )
| A、(-4,+∞) | ||
B、{a|a>-4,a≠3且a≠-
| ||
| C、(-∞,-4) | ||
D、(-∞,-4)∪(-
|
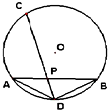 如图,AB,CD是⊙O的两条弦,它们相交于P,连结AD,BD.已知AD=BD=4,PC=6,那么CD的长为
如图,AB,CD是⊙O的两条弦,它们相交于P,连结AD,BD.已知AD=BD=4,PC=6,那么CD的长为