题目内容
已知直线l1：ax+（1-a）y=3与直线l2：（a-1）x+（2a+3）y=2，则a取何值时，直线l1与l2：（1）平行；（2）相交；（3）垂直．
考点：直线的一般式方程与直线的垂直关系,直线的一般式方程与直线的平行关系
专题：直线与圆
分析：（1）根据方程得出a（2a+3）-（1-a）（a-1）=0，2a-3（a-1）≠0，求解可判断平行的条件．
（2）利用相交得出：a（2a+3）-（1-a）（a-1）≠0，
（3）利用垂直得出：a（a-1）+（1-a）（2a+3）=0，求解即可．
（2）利用相交得出：a（2a+3）-（1-a）（a-1）≠0，
（3）利用垂直得出：a（a-1）+（1-a）（2a+3）=0，求解即可．
解答：
解：∵直线l1：ax+（1-a）y=3与直线l2：（a-1）x+（2a+3）y=2，
（1）∵直线l1与l2平行；
∴a（2a+3）-（1-a）（a-1）=0，2a-3（a-1）≠0，
3a2+a+1=0．无解，
∴a取任何值，直线l1与l2不平行；
（2）∵直线l1与l2相交，
∴a（2a+3）-（1-a）（a-1）≠0
即3a2+a+1≠0，恒成立，
∴a取任何值，直线l1与l2相交．
（3）∵l1，l2垂直．
∴a（a-1）+（1-a）（2a+3）=0
即a=1，或a=-3，
∴a=1，或a=-3，直线l1与l2垂直．
（1）∵直线l1与l2平行；
∴a（2a+3）-（1-a）（a-1）=0，2a-3（a-1）≠0，
3a2+a+1=0．无解，
∴a取任何值，直线l1与l2不平行；
（2）∵直线l1与l2相交，
∴a（2a+3）-（1-a）（a-1）≠0
即3a2+a+1≠0，恒成立，
∴a取任何值，直线l1与l2相交．
（3）∵l1，l2垂直．
∴a（a-1）+（1-a）（2a+3）=0
即a=1，或a=-3，
∴a=1，或a=-3，直线l1与l2垂直．
点评：本题考查两条直线的位置关系，用好直线的位置关系是解题的关键，考查计算能力．
练习册系列答案
相关题目
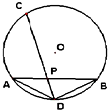如图，AB，CD是⊙O的两条弦，它们相交于P，连结AD，BD．已知AD=BD=4，PC=6，那么CD的长为
