题目内容

已知S=2t3，t=3，则
lim
△t→0
2(△t+3)3-2•33
△t
=
 
．
考点：极限及其运算
专题：导数的概念及应用
分析：根据题意，由导数在某一处的定义，求出计算结果．
解答： 解：∵S=2t3，
∴s′=6t2，
∴
lim
△t→0
2(△t+3)3-2•33
△t
=
lim
△t→0
s(△t+3)-s(3)
△t
=2S′|t=3=6×32=54，
故答案为：54
点评：本题考查了导数的定义的应用问题，解题时应明确导数的定义公式，从而得出计算结果，是基础题
练习册系列答案
相关题目
已知
a
=（
3
sinωx，-cosωx），
b
=（cosωx，cosωx），ω＞0，函数f(x)=
a
•
b
，且f（x）的图象相邻两条对称轴间的距离为
π
2
．
（Ⅰ）求函数f（x）的最小正周期和单调增区间；
（Ⅱ）已知△ABC的内角A，B，C所对的边分别为a，b，c，若a=
7
，b=2，且f（
A
2
）=
1
2
，求△ABC的面积．
已知角a∈（0，4π），且a与-
2
5
π的终边相同，则a=
 
．
2(1+i3)
(1+i)2
=
 
．
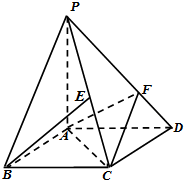如图，四棱锥P-ABCD的底面是边长为1的正方形，PA⊥CD，E为PC中点，PF=2FD，求证：BE∥平面AFC．
已知
a
=（4，-3），
b
=（2，2），若
a
+t
b
与
b
的夹角为45°，求实数t的值．
下列说法正确的个数为（　　）
①“x＞y”是“lgx＞lgy”的充要条件；
②“a＞b”是“ac2＞bc2”的必要不充分条件；
③“k=
3
”是“直线y=kx+2与圆x2+y2=1相切”的充分不必要条件；
④“α＞β”是“sinα＞sinβ”既不充分又不必要条件．
A、3 个
B、4 个
C、1 个
D、2个
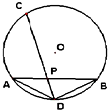 如图，AB，CD是⊙O的两条弦，它们相交于P，连结AD，BD．已知AD=BD=4，PC=6，那么CD的长为
 
．
把数列{
1
2n-1
}的所有数按照从大到小的原则写成如下数表．第k行有2k-1个数，第t行的第s个数（从左数起）记为A（t，s），则A（8，17）=
 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网