题目内容
10．若某几何体的三视图（单位：cm）如图所示，则该几何体的体积等于（ ）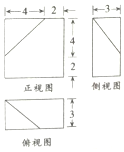
| A． | 84cm3 | B． | 92cm3 | C． | 98cm3 | D． | 100cm3 |
分析 由三视图，可得直观图是，长宽高分别为6，6，3的长方体，截去一个直三棱锥，侧棱长分别为4，4，3，利用体积公式求出该几何体的体积．
解答 解：由三视图，可得直观图是，长宽高分别为6，6，3的长方体，截去一个直三棱锥，侧棱长分别为4，4，3，
∴该几何体的体积等于$6×6×3-\frac{1}{3}×\frac{1}{2}×4×4×3$=100cm3，
故选D．
点评 本题考查了由三视图求几何体的体积，解题的关键是判断几何体的形状及数据所对应的几何量．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
1．
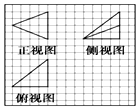如图，方格纸上正方形小格的边长为1，图中粗实线画出的是由一个正方体截得的一个几何体的三视图，则该几何体的体积为（ ）
如图，方格纸上正方形小格的边长为1，图中粗实线画出的是由一个正方体截得的一个几何体的三视图，则该几何体的体积为（ ）| A． | $\frac{16}{3}$ | B． | $\frac{32}{3}$ | C． | $\frac{64}{3}$ | D． | 32 |
5．某几何体的三视图如图所示，则此几何体的体积为（ ）
| A． | $\frac{4}{3}$ | B． | $\frac{8}{3}$ | C． | 4 | D． | 8 |
2．在极坐标系中，以下是圆ρ=2cosθ的一条切线的是（ ）
| A． | ρsinθ=2 | B． | ρsinθ=-2 | C． | ρcosθ=-2 | D． | ρcosθ=2 |
19．曲线y=x2的一种参数方程是（ ）
| A． | $\left\{{\begin{array}{l}{x={t^2}}\\{y={t^4}}\end{array}}\right.$ | B． | $\left\{{\begin{array}{l}{x=sint}\\{y={{sin}^2}t}\end{array}}\right.$ | C． | $\left\{{\begin{array}{l}{x=\sqrt{t}}\\{y=t}\end{array}}\right.$ | D． | $\left\{{\begin{array}{l}{x=t}\\{y={t^2}}\end{array}}\right.$ |