题目内容
20.自极点O任意作一条射线与直线ρcosθ=3相交于点M,在射线OM上取点P,使得|OM|•|OP|=12,求动点P的极坐标方程,并把它化为直角坐标方程.分析 设P(ρ,θ),M (ρ',θ),由于OM•OP=12,可得ρρ'=12.又ρ'cosθ=3,代入可得极坐标方程,利用互化公式即可得出.
解答 解:设P(ρ,θ),M(ρ′,θ).
∵|OM|•|OP|=12,∴ρρ′=12.
又ρ′cosθ=3,∴$\frac{12}{ρ}•cosθ=3$,则动点P的极坐标方程为ρ=4cosθ.…(5分)
极点在此曲线上,方程两边可同时乘ρ,得ρ2=4ρcosθ.
∴x2+y2-4x=0.…(10分)
点评 本题考查了极坐标方程化为直角坐标方程,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
10.若某几何体的三视图(单位:cm)如图所示,则该几何体的体积等于( )
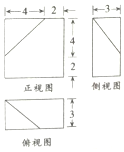

| A. | 84cm3 | B. | 92cm3 | C. | 98cm3 | D. | 100cm3 |
8.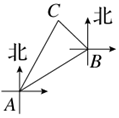 如图,某海上缉私小分队驾驶缉私艇以40km/h的速度由A出出发,沿北偏东60°方向进行海面巡逻,当航行半小时到达B处时,发现北偏西45°方向有一艘船C,若船C位于A的北偏东30°方向上,则缉私艇所在的B处与船C的距离是( )km.
如图,某海上缉私小分队驾驶缉私艇以40km/h的速度由A出出发,沿北偏东60°方向进行海面巡逻,当航行半小时到达B处时,发现北偏西45°方向有一艘船C,若船C位于A的北偏东30°方向上,则缉私艇所在的B处与船C的距离是( )km.
 如图,某海上缉私小分队驾驶缉私艇以40km/h的速度由A出出发,沿北偏东60°方向进行海面巡逻,当航行半小时到达B处时,发现北偏西45°方向有一艘船C,若船C位于A的北偏东30°方向上,则缉私艇所在的B处与船C的距离是( )km.
如图,某海上缉私小分队驾驶缉私艇以40km/h的速度由A出出发,沿北偏东60°方向进行海面巡逻,当航行半小时到达B处时,发现北偏西45°方向有一艘船C,若船C位于A的北偏东30°方向上,则缉私艇所在的B处与船C的距离是( )km.| A. | 5($\sqrt{6}$+$\sqrt{2}$) | B. | 5($\sqrt{6}$-$\sqrt{2}$) | C. | 10($\sqrt{6}$+$\sqrt{2}$) | D. | 10($\sqrt{6}$-$\sqrt{2}$) |
12.下列值为2的积分是( )
| A. | $\int_0^5{({2x-4})dx}$ | B. | $\int_0^π{cosxdx}$ | C. | $\int_1^3{\frac{1}{x}dx}$ | D. | $\int_0^π{sinxdx}$ |