题目内容
15．已知函数$f（x）=\left\{\begin{array}{l}3x-\frac{1}{2}，x＜1\\{2^x}，x≥1\end{array}\right.$，则$f[f（\frac{1}{2}）]$=2．分析 由已知中$f（x）=\left\{\begin{array}{l}3x-\frac{1}{2}，x＜1\\{2^x}，x≥1\end{array}\right.$，将x=$\frac{1}{2}$代入计算，可得答案．
解答 解：∵$f（x）=\left\{\begin{array}{l}3x-\frac{1}{2}，x＜1\\{2^x}，x≥1\end{array}\right.$，
∴f（$\frac{1}{2}$）=1，
$f[f（\frac{1}{2}）]$=f（1）=2
故答案为：2
点评 本题考查的知识点是函数求值，分段函数的应用，难度不大，属于基础题．
练习册系列答案
相关题目
如图，在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水，将容器底面一边BC固定于地面上，再将容器倾斜，随着倾斜度的不同，有下列四个说法：
小晶用圆、三角形、正方形按一定规律画图，前八个图形如图所示，则猜测第2017个图形中共含有的正方形个数为336．
10．若某几何体的三视图（单位：cm）如图所示，则该几何体的体积等于（ ）
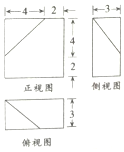
| A． | 84cm3 | B． | 92cm3 | C． | 98cm3 | D． | 100cm3 |
20．在平面直角坐标系中，方程x2+y2=1经过伸缩变换$\left\{\begin{array}{l}{{x}^{′}=2x}\\{{y}^{′}=3y}\end{array}\right.$后，得到的方程为（ ）
| A． | $\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{3}$=1 | B． | 2x2+3y2=1 | C． | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{9}$=1 | D． | 4x2+9y2=1 |
