题目内容
18.已知曲线C的极坐标方程是ρ-2cosθ-4sinθ=0,以极点为在平面直角坐标系的原点,极轴为x轴的正半轴建立平面直角坐标系xoy,直线的参数方程为$\left\{\begin{array}{l}x=\frac{{\sqrt{3}}}{2}t\\ y=1+\frac{1}{2}t\end{array}\right.$(t为参数).(1)将曲线C的极坐标方程化为直角坐标方程,将直线l的参数方程化为普通方程;
(2)若直线l与曲线C相交于A,B两点,与y轴交于点M,求(|MA|+|MB|)2的值.
分析 (1)按要求将极坐标方程即参数方程化为普通方程;
(2)利用直线的参数方程代入曲线的普通方程,利用韦达定理求线段的长度.
解答 解:(1)曲线C的极坐标方程是ρ-2cosθ-4sinθ=0,化为直角坐标方程为
x2+y2-2x-4y=0,直线l的普通方程为x-$\sqrt{3}$y+$\sqrt{3}$=0. …(5分)
(2)将l的参数方程代入曲线C的直角坐标方程,得t2-($\sqrt{3}$+1)t-3=0,
点M对应的参数t=0,设点A、B对应的参数分别为t1,t2,
则${t}_{1}+{t}_{2}=\sqrt{3}+1$,t1•t2=-3,
所以|MA|+|MB|=|t1|+|t2|=|t1-t2|=$\sqrt{({t}_{1}+{t}_{2})^{2}-4{t}_{1}{t}_{2}}$=$\sqrt{16+2\sqrt{3}}$
所以(|MA|+|MB|)2=16+2$\sqrt{3}$. …(10分)
点评 本题考查了曲线的极坐标方程、直线的参数方程化为普通方程以及直线与曲线相交;属于中档题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
13.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
10.若某几何体的三视图(单位:cm)如图所示,则该几何体的体积等于( )
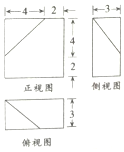

| A. | 84cm3 | B. | 92cm3 | C. | 98cm3 | D. | 100cm3 |
8.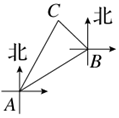 如图,某海上缉私小分队驾驶缉私艇以40km/h的速度由A出出发,沿北偏东60°方向进行海面巡逻,当航行半小时到达B处时,发现北偏西45°方向有一艘船C,若船C位于A的北偏东30°方向上,则缉私艇所在的B处与船C的距离是( )km.
如图,某海上缉私小分队驾驶缉私艇以40km/h的速度由A出出发,沿北偏东60°方向进行海面巡逻,当航行半小时到达B处时,发现北偏西45°方向有一艘船C,若船C位于A的北偏东30°方向上,则缉私艇所在的B处与船C的距离是( )km.
 如图,某海上缉私小分队驾驶缉私艇以40km/h的速度由A出出发,沿北偏东60°方向进行海面巡逻,当航行半小时到达B处时,发现北偏西45°方向有一艘船C,若船C位于A的北偏东30°方向上,则缉私艇所在的B处与船C的距离是( )km.
如图,某海上缉私小分队驾驶缉私艇以40km/h的速度由A出出发,沿北偏东60°方向进行海面巡逻,当航行半小时到达B处时,发现北偏西45°方向有一艘船C,若船C位于A的北偏东30°方向上,则缉私艇所在的B处与船C的距离是( )km.| A. | 5($\sqrt{6}$+$\sqrt{2}$) | B. | 5($\sqrt{6}$-$\sqrt{2}$) | C. | 10($\sqrt{6}$+$\sqrt{2}$) | D. | 10($\sqrt{6}$-$\sqrt{2}$) |
 小晶用圆、三角形、正方形按一定规律画图,前八个图形如图所示,则猜测第2017个图形中共含有的正方形个数为336.
小晶用圆、三角形、正方形按一定规律画图,前八个图形如图所示,则猜测第2017个图形中共含有的正方形个数为336.