题目内容
2.在极坐标系中,以下是圆ρ=2cosθ的一条切线的是( )| A. | ρsinθ=2 | B. | ρsinθ=-2 | C. | ρcosθ=-2 | D. | ρcosθ=2 |
分析 圆的直角坐标方程为(x-1)2+y2=1.由此能求出圆ρ=2cosθ的一条切线方程.
解答 解:圆ρ=2cosθ,即ρ2=2ρcosθ,
由ρ2=x2+y2,ρcosθ=x,
得x2+y2=2x,即(x-1)2+y2=1.
在A中,ρsinθ=2,即y=2,圆心(1,0)到直线y=2的距离d=2>r=1,故A不是圆的切线;
在B中,ρsinθ=-2,即y=-2,圆心(1,0)到直线y=-2的距离d=2>r=1,故B不是圆的切线;
在C中,ρcosθ=-2,即x=-2,圆心(1,0)到直线x=-2的距离d=3>r=1,故C不是圆的切线;
在D中,ρcosθ=2,即x=2,圆心(1,0)到直线x=2的距离d=1=r,故D是圆的切线.
故选:D.
点评 本题考查圆的切线方程的求法,考查极坐标、直角坐标的互化,考查推理论证能力、运算求解能力,考查转化化归思想、数形结合思想,是中档题.

练习册系列答案
相关题目
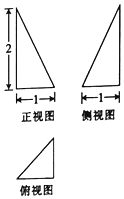
13.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
10.若某几何体的三视图(单位:cm)如图所示,则该几何体的体积等于( )
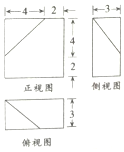

| A. | 84cm3 | B. | 92cm3 | C. | 98cm3 | D. | 100cm3 |
17.若$\frac{1}{1+a}>1-a$,则实数a的取值范围是( )
| A. | a>0 | B. | a>1 | C. | a>-1且a≠0 | D. | a<0 |
12.下列值为2的积分是( )
| A. | $\int_0^5{({2x-4})dx}$ | B. | $\int_0^π{cosxdx}$ | C. | $\int_1^3{\frac{1}{x}dx}$ | D. | $\int_0^π{sinxdx}$ |