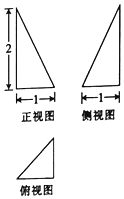
题目内容
20.已知直线l的极坐标方程为ρsin(θ+$\frac{π}{3}$)=$\sqrt{3}$,曲线C的参数方程为$\left\{\begin{array}{l}{x=2cosφ}\\{y=sinφ}\end{array}\right.$.(φ为参数)(1)写出直线l的直角坐标方程和曲线C的普通方程;
(2)求直线l被曲线C截得的弦长.
分析 (1)由x=ρcosθ,y=ρsinθ,能求出直线l的直角坐标方程,曲线C的参数方程消去参数φ能求出曲线C的普通方程.
(2)联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+{y}^{2}=1}\\{\sqrt{3}x+y-2\sqrt{3}=0}\end{array}\right.$,得13x2-48x+44=0,由此利用根的判别式、韦达定理、参数方程能求出弦长|AB|.
解答 解:(1)∵直线l的极坐标方程为ρsin(θ+$\frac{π}{3}$)=$\sqrt{3}$,
∴$ρ(sinθcos\frac{π}{3}+cosθsin\frac{π}{3})$=$\frac{1}{2}ρsinθ+\frac{\sqrt{3}}{2}ρcosθ$=$\sqrt{3}$,
∴直线l的直角坐标方程为$\sqrt{3}x+y$-2$\sqrt{3}$=0.
∵曲线C的参数方程为$\left\{\begin{array}{l}{x=2cosφ}\\{y=sinφ}\end{array}\right.$.(φ为参数)
∴消去参数φ得曲线C的普通方程为:
$\frac{{x}^{2}}{4}+{y}^{2}$=1.
(2)联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+{y}^{2}=1}\\{\sqrt{3}x+y-2\sqrt{3}=0}\end{array}\right.$,得13x2-48x+44=0,
△=(-48)2-4×13×44=16,
${x}_{1}+{x}_{2}=\frac{48}{13}$,${x}_{1}{x}_{2}=\frac{44}{13}$,
∴弦长|AB|=$\sqrt{1+(-\sqrt{3})^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$
=2$\sqrt{(\frac{48}{13})^{2}-4×\frac{44}{13}}$=2×$\frac{4}{13}$=$\frac{8}{13}$.
点评 本题考查直线的直角坐标方程,曲线的普通方程的求法,考查弦长的求法,是中档题,解题时要认真审题,注意极坐标、直角坐标互化公式、韦达定理、弦长公式的合理运用.

 口算题天天练系列答案
口算题天天练系列答案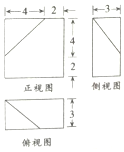
| A. | 84cm3 | B. | 92cm3 | C. | 98cm3 | D. | 100cm3 |
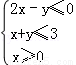 ,则目标函数z=2x+y的最大值为( )
,则目标函数z=2x+y的最大值为( ) 如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:
如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法: