Question

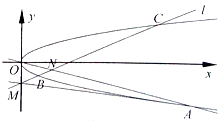在平面直角坐标系xOy中，已知抛物线y²=2px（p＞0）的准线方程为 x=-

1

4

，过点M（0，-2）作抛物线的切线MA，切点为A（异于点O）．直线l过点M与抛物线交于两点B，C，与直线OA交于点N．
（1）求抛物线的方程；
（2）试问：

MN

MB

+

MN

MC

的值是否为定值？若是，求出定值；若不是，说明理由．

Answer 1

考点：抛物线的简单性质

专题：计算题,直线与圆,圆锥曲线的定义、性质与方程

分析：（1）由抛物线的准线方程可得p，进而得到抛物线方程；
（2）求出函数y=-

x

的导数，求出切线的斜率，以及切线方程，联立切线方程和抛物线方程求得切点A，进而直线OA的方程，设出直线BC的方程，联立抛物线方程运用韦达定理，求出N的坐标，代入所求式子化简即可得到定值2．

解答： 解：（1）由题设知，-

p

2

=-

1

4

，即p=

1

2

，
所以抛物线的方程为y²=x；
（2）因为函数y=-

x

的导函数为y′=-

1

2 x

，
设A（x₀，y₀），则直线MA的方程为y-y0=-

1

2 x0

(x-x0)，
因为点M（0，-2）在直线MA上，所以-2-y₀=-

1

2 x0

•（-x₀）．
联立

y0=-2- 1 2 x0 y02=x0

，解得A（16，-4），
所以直线OA的方程为y=-

1

4

x． 
设直线BC方程为y=kx-2，
由

y2=x y=kx-2

，得k²x²-（4k+1）x+4=0，
所以xB+xC=

4k+1

k2

，xBxC=

4

k2

．
由

y=- 1 4 x y=kx-2

，得xN=

8

4k+1

．
所以

MN

MB

+

MN

MC

=

xN

xB

+

xN

xC

=xN×

xB+xC

xBxC

=

8

4k+1

×

4k+1 k2

4 k2

=

8

4k+1

×

4k+1

4

=2，
故

MN

MB

+

MN

MC

的为定值2．

点评：本题考查抛物线的方程和性质，考查直线方程和抛物线方程联立，运用韦达定理，以及导数的运用：求切线方程，考查运算能力，属于中档题和易错题．