题目内容
若方程
-
=1表示双曲线,则k的取值范围是( )
| x2 |
| k |
| y2 |
| k-2 |
| A、k>2 | B、k<0 |
| C、k>2,或k<0 | D、0<k<2 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:讨论双曲线的焦点,当焦点在x轴上,有k>0且k-2>0;焦点在y轴上,有2-k>0,且-k>0,分别解出它们,再求并集即可.
解答:
解:若方程
-
=1表示双曲线,
则当焦点在x轴上,有k>0且k-2>0,
解得,k>2;
当焦点在y轴上,则有
-
=1,
具有2-k>0,且-k>0,
解得,k<0,
则有k>2或k<0.
故选C.
| x2 |
| k |
| y2 |
| k-2 |
则当焦点在x轴上,有k>0且k-2>0,
解得,k>2;
当焦点在y轴上,则有
| y2 |
| 2-k |
| x2 |
| -k |
具有2-k>0,且-k>0,
解得,k<0,
则有k>2或k<0.
故选C.
点评:本题考查双曲线的方程,考查分类讨论的思想方法,考查运算能力,属于基础题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
已知向量
,
满足
⊥
,|
|=1,|
|=2,则|2
-
|=( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、2
| ||
B、2
| ||
| C、8 | ||
| D、12 |
如果实数x,y满足等式(x-2)2+y2=3,那么
的最大值是( )
| y |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设F为双曲线
-
=1(a>0,b>0)的右焦点,P是双曲线上的点,若它的渐近线上存在一点Q(在第一象限内),使得
=2
,则双曲线离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| FP |
| PQ |
| A、(1,3) |
| B、(3,+∞) |
| C、(1,2) |
| D、(2,+∞) |
若数列{an}的前n项的和Sn=3n-2,那么这个数列的通项公式为( )
A、an=(
| |||||||
B、an=an=3×(
| |||||||
| C、an=3n-2 | |||||||
D、an=
|
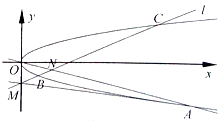 在平面直角坐标系xOy中,已知抛物线y2=2px(p>0)的准线方程为 x=-
在平面直角坐标系xOy中,已知抛物线y2=2px(p>0)的准线方程为 x=-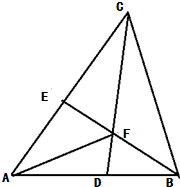 在△ABC中,∠A=60°,AB=3,AC=5,BD=1,CE=2.
在△ABC中,∠A=60°,AB=3,AC=5,BD=1,CE=2.