题目内容
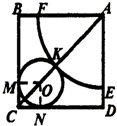 如图所示,在边长为
如图所示,在边长为| 2 |
考点:旋转体(圆柱、圆锥、圆台)
专题:空间位置关系与距离
分析:由已知中边长为5+
的正方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,且以扇形为圆锥的侧面,以圆O为圆锥底面,可围成一个圆锥,设圆锥的母线长为l,底面半径为r,求出l,r后,代入圆锥表面积公式,可以得到答案.
| 2 |
解答:
解:设圆锥的母线长为l,底面半径为r,高为h,
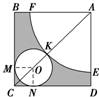
由已知条件可得:
,
解得r=
,l=4
,
∴S=πrl+πr2=10π,
故答案为:10π;

由已知条件可得:
|
解得r=
| 2 |
| 2 |
∴S=πrl+πr2=10π,
故答案为:10π;
点评:本题考查的知识点是圆锥的表面积,其中根据已知构造方程,求出圆锥的母线长l,底面半径r,是解答的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
设F为双曲线
-
=1(a>0,b>0)的右焦点,P是双曲线上的点,若它的渐近线上存在一点Q(在第一象限内),使得
=2
,则双曲线离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| FP |
| PQ |
| A、(1,3) |
| B、(3,+∞) |
| C、(1,2) |
| D、(2,+∞) |
正方体的内切球的体积为36π,则此正方体的表面积是(V球体=
πR3(R为球的半径))( )
| 4 |
| 3 |
| A、216 | B、72 |
| C、108 | D、648 |
点A(1,3)关于直线y=kx+b的对称点是B(-2,1),则直线y=kx+b在x轴上的截距是( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
若数列{an}的前n项的和Sn=3n-2,那么这个数列的通项公式为( )
A、an=(
| |||||||
B、an=an=3×(
| |||||||
| C、an=3n-2 | |||||||
D、an=
|
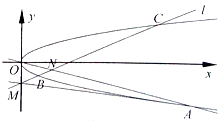 在平面直角坐标系xOy中,已知抛物线y2=2px(p>0)的准线方程为 x=-
在平面直角坐标系xOy中,已知抛物线y2=2px(p>0)的准线方程为 x=-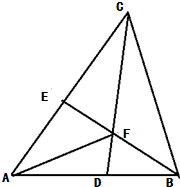 在△ABC中,∠A=60°,AB=3,AC=5,BD=1,CE=2.
在△ABC中,∠A=60°,AB=3,AC=5,BD=1,CE=2.