题目内容
 如图是某几何体的三视图,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的体积是( )
如图是某几何体的三视图,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的体积是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:根据几何体的三视图,得出该几何体的结构特征,从而求出它的体积.
解答:
解:根据几何体的三视图,得;
该几何体是底面为半圆,母线长为2的半圆锥体;
且底面半圆的半径为1,
∴该半圆锥个高为2×
=
,
它的体积为V=
×
π•12×
=
π.
故选:C.
该几何体是底面为半圆,母线长为2的半圆锥体;
且底面半圆的半径为1,
∴该半圆锥个高为2×
| ||
| 2 |
| 3 |
它的体积为V=
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
| ||
| 6 |
故选:C.
点评:本题考查了空间几何体的三视图的应用问题,是基础题目.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
 如图,一个水平放置的平面图形的斜二测直观图是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是( )
如图,一个水平放置的平面图形的斜二测直观图是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是( )A、
| ||||||
B、1+
| ||||||
C、1+
| ||||||
D、2+
|
已知向量
,
满足
⊥
,|
|=1,|
|=2,则|2
-
|=( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、2
| ||
B、2
| ||
| C、8 | ||
| D、12 |
点A(1,3)关于直线y=kx+b的对称点是B(-2,1),则直线y=kx+b在x轴上的截距是( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
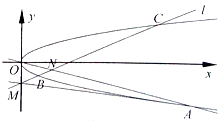 在平面直角坐标系xOy中,已知抛物线y2=2px(p>0)的准线方程为 x=-
在平面直角坐标系xOy中,已知抛物线y2=2px(p>0)的准线方程为 x=-