题目内容
 先阅读下面的文字,再按要求解答.
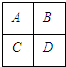
先阅读下面的文字,再按要求解答.如图,在一个田字形地块的A、B、C、D四个区域中栽种观赏植物,要求同一区域种同一种植物,相邻两区域(A与D,B与C不相邻)种不同的植物,现有四种不同的植物可供选择,问不同的种植方案有多少种?
某学生给出如下的解答:
解:完成四个区域种植植物这件事,可分4步:
第一步:在区域A种植物,有C
1 4 |
第二步:在区域B种植与区域A不同的植物,有C
1 3 |
第三步:在区域D种植与区域B不同的植物,有C
1 3 |
第四步:在区域C种植与区域A、D均不同的植物,有C
1 2 |
根据分步计数原理,共有C
1 4 |
1 3 |
1 3 |
1 2 |
答:共有72种不同的种植方案.
问题:
(1)请你判断上述的解答是否正确,并说明理由;
(2)请写出你解答本题的过程.
考点:计数原理的应用
专题:排列组合
分析:(1)上述解答不正确,A、D两区域中可以种植不同植物,也可以种植相同的植物.
(2)在A、B、C、D四个区域完成种植植物这件事,可分为A、D两区域种植同一种植物和A、D两区域种植不同种植物两类,根据分类加法计数原理可得.
(2)在A、B、C、D四个区域完成种植植物这件事,可分为A、D两区域种植同一种植物和A、D两区域种植不同种植物两类,根据分类加法计数原理可得.
解答:
解:(1)上述解答不正确.
理由如下:上述解答中的第四步认为A、D区域种植的植物一定是不同的,事实上,已知条件中规定A、D两区域不相邻,所以A、D两区域中可以种植不同植物,也可以种植相同的植物,故解答不正确.
正确解答:以种植需要进行合理的分类.
(2)在A、B、C、D四个区域完成种植植物这件事,可分为A、D两区域种植同一种植物和A、D两区域种植不同种植物两类.
①A、D两区域种植同一种植物的方法有
•
•
=36(种)
②A、D两区域种植不同种植物的方法有
•
•
•
=48(种)
根据分类加法计数原理可知,符合题意的种植方法共有36+48=84(种)
答:共有84种不同的种植方案.
理由如下:上述解答中的第四步认为A、D区域种植的植物一定是不同的,事实上,已知条件中规定A、D两区域不相邻,所以A、D两区域中可以种植不同植物,也可以种植相同的植物,故解答不正确.
正确解答:以种植需要进行合理的分类.
(2)在A、B、C、D四个区域完成种植植物这件事,可分为A、D两区域种植同一种植物和A、D两区域种植不同种植物两类.
①A、D两区域种植同一种植物的方法有
| C | 1 4 |
| C | 1 3 |
| C | 1 3 |
②A、D两区域种植不同种植物的方法有
| C | 1 4 |
| C | 1 3 |
| C | 1 2 |
| C | 1 2 |
根据分类加法计数原理可知,符合题意的种植方法共有36+48=84(种)
答:共有84种不同的种植方案.
点评:对于复杂一点的计数问题,有时分类以后,每类方法并不都是一步完成的,必须在分类后又分步,综合利用两个原理解决,即类中有步,步中有类.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=