题目内容

已知函数f（x）=
cos4x-1
2cos(
π
2
+2x)
+cos2x-sin2x．
（1）求函数f（x）的最小正周期和单调递减区间；
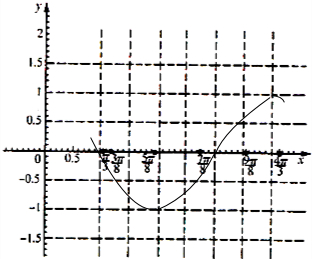
（2）在所给坐标系中画出函数在区间[
π
3
，
4π
3
]的图象（用五点法作图）．
考点：三角函数中的恒等变换应用,三角函数的周期性及其求法,由y=Asin（ωx+φ）的部分图象确定其解析式
专题：三角函数的图像与性质
分析：（1）利用二倍角公式和两角和公式对函数解析式化简，根据周期公式求得最小正周期，根据正弦函数的单调性求得函数的单调减区间．
（2）利用五点法作图．
解答： 解：（1）f（x）=
cos4x-1
2cos(
π
2
+2x)
+cos2x-sin2x=
-2sin22x
-2sin2x
+cos2x=sin2x+cos2x=
2
sin（2x+
π
4
），
∴T=
2π
2
=π，
由2kπ+
π
2
≤2x+
π
4
≤2kπ+
3π
2
，得kπ+
π
8
≤x≤kπ+
5π
8
，k∈Z，
∴函数的单调减区间为[kπ+
π
8
，kπ+
5π
8
]（k∈Z）．
（2）五点列表如下
x -
π
8
π
8
3π
8
5π
8
7π
8
y 0 1 0 -1 0
点评：本题主要考查了三角函数恒等变换的应用，三角函数图象与性质．考查学生对三角函数基础知识的理解和应用．
练习册系列答案
相关题目
已知AB，BC，CD为两两垂直的三条线段，且它们的长都等于1，则AD的长为（　　）
A、1
B、2
C、3
D、
3
已知函数f（x）=（ax+1）ex
（Ⅰ）若a=-1，求函数f（x）的单调区间；
（Ⅱ）当a＞0时，求函数f（x）在[-2，0]的最小值；
（Ⅲ）设n∈N，a=0，F（x）=f（x）-x，求证：
(n+1)(n+2)
2
＜
en+1
e-1
．
设函数f（x）=
3
cos2ωx+sinωxcosωx+a（其中ω＞0，a∈R），且f（x）的最小正周期为π．
（1）求ω的值；
（2）如果f（x）在区间[-
π
6
，
5π
12
]上的最小值为
3
2
，求a的值．
已知
a
=（2cosx，1），
b
=（cosx，
3
sin2x+m），f（x）=
a
•
b
；
（1）求函数在[0，π]上的单调增区间；
（2）当x∈[0，
π
6
]时，f（x）的最大值为4，求实数m的值．（提示：
a
•
b
=x1x2+y1y2）
四棱锥P-ABCD的底面是边长为a的正方形，侧棱PA⊥底面ABCD，在侧面PBC内有BE⊥PC于E，且BE=
6
3
a．
（1）试在AB上找一点F，使EF∥平面PAD．
（2）在平面PAD上是否存在一点G，使GE⊥PBC．
已知
a
=（1，1），
b
=（-2，2），
c
=（2，k）．
（1）若（
a
-
b
）∥
c
，求k的值．
（2）若
a
⊥
c
，求k的值．
（3）若
a
与 
c
的夹角为锐角，求k的取值范围．
先阅读下面的文字，再按要求解答．
如图，在一个田字形地块的A、B、C、D四个区域中栽种观赏植物，要求同一区域种同一种植物，相邻两区域（A与D，B与C不相邻）种不同的植物，现有四种不同的植物可供选择，问不同的种植方案有多少种？
某学生给出如下的解答：
解：完成四个区域种植植物这件事，可分4步：
第一步：在区域A种植物，有C
 
1
4
种方法；
第二步：在区域B种植与区域A不同的植物，有C
 
1
3
种方法；
第三步：在区域D种植与区域B不同的植物，有C
 
1
3
种方法；
第四步：在区域C种植与区域A、D均不同的植物，有C
 
1
2
种方法．
根据分步计数原理，共有C
 
1
4
C
 
1
3
C
 
1
3
C
 
1
2
=72（种）．
答：共有72种不同的种植方案．
问题：
（1）请你判断上述的解答是否正确，并说明理由；
（2）请写出你解答本题的过程．
设△ABC的内角A，B，C所对的边长分别为a，b，c，且cosB=
4
5
，b=2．
（1）当A=45°时，求a的值；
（2）当a+c的值为2
10
时，求△ABC的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网