题目内容
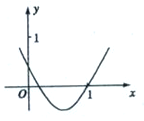 函数f(x)=x2-bx+a的图象如图所示,则函数g(x)=lnx+f′(x)的零点所在的区间是( )
函数f(x)=x2-bx+a的图象如图所示,则函数g(x)=lnx+f′(x)的零点所在的区间是( )A、(
| ||||
B、(
| ||||
| C、(1,2) | ||||
| D、(2,3) |
考点:函数的单调性与导数的关系,平面向量数量积的坐标表示、模、夹角
专题:计算题,数形结合,函数的性质及应用
分析:由二次函数图象的对称轴确定b的范围,据g(x)的表达式计算g(
)和g(1)的值的符号,从而确定零点所在的区间.
| 1 |
| 2 |
解答:
解:∵二次函数f(x)图象的对称轴 x=
∈(
,1),
∴1<b<2,g(x)=lnx+2x-b在定义域内单调递增,
g(
)=ln
+1-b<0,
g(1)=ln1+2-b=2-b>0,
∴函数g(x)=lnx+f′(x)的零点所在的区间是(
,1);
故选:B.
| b |
| 2 |
| 1 |
| 2 |
∴1<b<2,g(x)=lnx+2x-b在定义域内单调递增,
g(
| 1 |
| 2 |
| 1 |
| 2 |
g(1)=ln1+2-b=2-b>0,
∴函数g(x)=lnx+f′(x)的零点所在的区间是(
| 1 |
| 2 |
故选:B.
点评:本题主要考察了导数的运算、函数零点的判断以及识图能力,体现了数形结合的思想,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=|2x-1|,a<b<c,且f(a)>f(c)>f(b),则下列结论中成立的是( )
| A、a<0,b<0,c<0 |
| B、a<0,b≥0,c>0 |
| C、2-a<2c |
| D、2a+2c<2 |
已知函数f(x)的定义域为R,对任意实数m,n都满足 f(m+n)=f(m)+f(n)-1,当x>0时,f(x)>1,则不等式f(2x-1)+f(
)<2的解集是( )
| 1 |
| x |
A、(-∞,-
| ||
| B、(-∞,0) | ||
| C、(0,+∞) | ||
D、(-∞,-
|
若直线(a2+4a+3)x+(a2+a-6)y-6=0与x-2y-1=0垂直,则a等于( )
| A、.5 | B、.5或-3 |
| C、.-3 | D、不存在 |
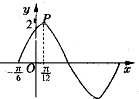 已知函数f(x)=2sin(ωx+φ),(ω>0,φ∈(0,
已知函数f(x)=2sin(ωx+φ),(ω>0,φ∈(0,