题目内容
若M，A，B三点不共线，且存在实数λ1，λ2，使
=λ1
+λ2
，求证：“C为A，B的中点”的充要条件是“λ1=λ2=
”
| MC |
| MA |
| MB |
| 1 |
| 2 |
考点：必要条件、充分条件与充要条件的判断
专题：证明题,简易逻辑
分析：充要性证明一般分充分性与必要性分开证明，由
=
+
可推出
+
=0，由C为A，B的中点可推出
=
+
．
| MC |
| 1 |
| 2 |
| MA |
| 1 |
| 2 |
| MB |
| CA |
| CB |
| MC |
| 1 |
| 2 |
| MA |
| 1 |
| 2 |
| MB |
解答：
解：充分性：∵λ1=λ2=
，
∴
=
+
，
即
（
-
）+
（
-
）=0，
即
+
=0，
∴C为A，B的中点；
必要性：∵C为A，B的中点，
∴
+
=0，
∴
（
-
）+
（
-
）=0，
∴
=
+
，
又∵M，A，B三点不共线，
∴
，
是平面向量的一组基底，
∴λ1=λ2=
．
| 1 |
| 2 |
∴
| MC |
| 1 |
| 2 |
| MA |
| 1 |
| 2 |
| MB |
即
| 1 |
| 2 |
| MA |
| MC |
| 1 |
| 2 |
| MB |
| MC |
即
| CA |
| CB |
∴C为A，B的中点；
必要性：∵C为A，B的中点，
∴
| CA |
| CB |
∴
| 1 |
| 2 |
| MA |
| MC |
| 1 |
| 2 |
| MB |
| MC |
∴
| MC |
| 1 |
| 2 |
| MA |
| 1 |
| 2 |
| MB |
又∵M，A，B三点不共线，
∴
| MA |
| MB |
∴λ1=λ2=
| 1 |
| 2 |
点评：本题考查了充要性的证明，充要性证明一般分充分性与必要性分开证明；同时考查了向量的化简，由
+
=0可知C为A，B的中点，由
=
+
，
=λ1
+λ2
；由平面向量基本定理可知λ1=λ2=
．属于基础题．
| CA |
| CB |
| MC |
| 1 |
| 2 |
| MA |
| 1 |
| 2 |
| MB |
| MC |
| MA |
| MB |
| 1 |
| 2 |
练习册系列答案
相关题目
已知函数f（x）=|2x-1|，a＜b＜c，且f（a）＞f（c）＞f（b），则下列结论中成立的是（ ）
| A、a＜0，b＜0，c＜0 |
| B、a＜0，b≥0，c＞0 |
| C、2-a＜2c |
| D、2a+2c＜2 |
已知函数f（x）的定义域为R，对任意实数m，n都满足 f（m+n）=f（m）+f（n）-1，当x＞0时，f（x）＞1，则不等式f（2x-1）+f（
）＜2的解集是（ ）
| 1 |
| x |
A、（-∞，-
| ||
| B、（-∞，0） | ||
| C、（0，+∞） | ||
D、（-∞，-
|
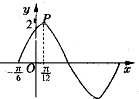已知函数f（x）=2sin（ωx+φ），（ω＞0，φ∈（0，