题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c.设函数f(x)=2sin(
+
)cos
+
,x∈R,若f(A)=
.
(Ⅰ)求角A的大小;
(Ⅱ)当a=14,b=10时,求△ABC的面积.
| x |
| 2 |
| π |
| 6 |
| x |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
(Ⅰ)求角A的大小;
(Ⅱ)当a=14,b=10时,求△ABC的面积.
考点:余弦定理的应用,三角函数中的恒等变换应用
专题:计算题,三角函数的求值,解三角形
分析:(Ⅰ)运用两角和的正弦公式和二倍角的正弦、余弦公式,即可化简f(x),再由f(A)=
,即可得到A;
(Ⅱ)由余弦定理得到c,再由面积公式,即可得到.
| 3 |
| 2 |
(Ⅱ)由余弦定理得到c,再由面积公式,即可得到.
解答:
解:(Ⅰ)f(x)=
sin
cos
+cos2
+
=
sinx+
cosx+1=sin(x+
)+1;
由f(A)=
,得sin(A+
)=
,
又
<A+
<
,
则A+
=
,故A=
;
(Ⅱ)由余弦定理得:142=102+c2-2×10c×cos120°,
即c2+10c-96=0,得c=6,
则S△ABC=
bcsinA=15
.
| 3 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| 1 |
| 2 |
=
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
由f(A)=
| 3 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
又
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
则A+
| π |
| 6 |
| 5π |
| 6 |
| 2π |
| 3 |
(Ⅱ)由余弦定理得:142=102+c2-2×10c×cos120°,
即c2+10c-96=0,得c=6,
则S△ABC=
| 1 |
| 2 |
| 3 |
点评:本题考查三角函数的化简和求值,考查和差公式和二倍角公式的运用,同时考查余弦定理和面积公式的运用,考查运算能力,属于中档题.

练习册系列答案
相关题目
设
、
、
是单位向量,若
+
=
,则
•
的值为( )
| a |
| b |
| c |
| a |
| b |
| 2 |
| c |
| a |
| c |
A、
| ||||
B、-
| ||||
| C、1 | ||||
| D、-1 |
3名大学生分配到4个单位实习,每个单位不超过2名学生,则不同的分配方案有( )
| A、10种 | B、36种 |
| C、48种 | D、60种 |
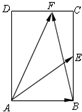 如图,在矩形ABCD中,AB=2,BC=2
如图,在矩形ABCD中,AB=2,BC=2