题目内容

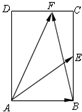如图，在矩形ABCD中，AB=2，BC=2
2
点E为BC的中点，点F在边CD上，若
AB
•
AF
=2，则
AE
•
BF
的值是
 
．
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：建立直角坐标系，由已知条件可得F的坐标，进而可得向量
AE
和
BF
的坐标，可得数量积．
解答： 解：建立如图所示的坐标系，可得A（0，0），
B（2，0），E（2，
2
），F（x，2
2
），
AB
•
AF
=（2，0）•（x，2
2
）=2x=2，
即有x=1．
即F（1，2
2
），
BF
=（-1，2
2
），
则
AE
•
BF
=（2，
2
）•（-1，2
2
）
=-2+4=2．
故答案为：2．
点评：本题考查平面向量的数量积的坐标公式，考查运用坐标法解题，考查运算能力，属于中档题．
练习册系列答案
相关题目
已知数列{an}满足an+1=6an+2n+1，a1=1．
（1）求证：数列{
an
2n
+
1
2
}是等比数列；
（2）若数列{an+r2n}是等比数列，求r；
（3）求
an
2
．
直线2x+y-10=0与不等式组
x≥0
y≥0
x-y≥-2
4x+3y≤20
表示平面区域的公共点有
 
个．
设函数f（x）=
x
a(x+2)
，方程x=f（x）有唯一解，其中实数a为常数，f（x1）=
2
2013
，f（xn）=xn+1（n∈N*）．
（1）求f（x）的表达式；
（2）求x2015的值；
（3）若an=
4
xn
-4023且bn=
a
2
n+1
+
a
2
n
2an+1an
（n∈N*），求证：b1+b2+…+bn＜n+1．
设关于x的不等式x2-2x-（a2-2a）＜0的解集为A，若2∈A，则实数a的取值范围为（　　）
A、（0，2）
B、（-∞，0）
C、（2，+∞）
D、（-∞，0）∪（2，+∞）
在△ABC中，角A，B，C所对的边分别为a，b，c．设函数f(x)=2sin(
x
2
+
π
6
)cos
x
2
+
1
2
，x∈R，若f（A）=
3
2
．
（Ⅰ）求角A的大小；
（Ⅱ）当a=14，b=10时，求△ABC的面积．
已知数列{an}满足：a1=a，an+1=
1
2
an2-an+2，其中n∈N*．
（Ⅰ）是否存在实数a使得{an}为等差数列，若存在，求出a的值，若不存在，请说明理由；
（Ⅱ）当a=4时，证明：
1
a1
+
1
a2
+…+
1
an
＜
1
2
．
已知函数f（x）=|logax|．
（1）当a=2时，求函数f（x）-3的零点；
（2）若存在互不相等的正实数m，n，使f（m）=f（n），判断函数g（x）=mx+nx-1的奇偶性，并证明你的结论；
（3）在（2）的条件下，若m＞n，当x＞m时，求函数y=logmxlognx+logmx的值域．
设a是实数，且
1+i
i
+
ai
1-i
（i是虚数单位）是实数，则a=（　　）
A、2
B、
3
2
C、1
D、
1
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网