题目内容
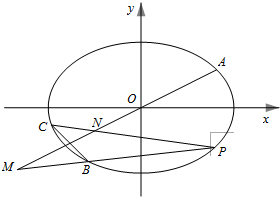 如图,在平面直角坐标系xOy中,已知A,B,C是椭圆
如图,在平面直角坐标系xOy中,已知A,B,C是椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
3
| ||
| 2 |
(1)求椭圆的标准方程;
(2)求点C的坐标;
(3)设动点P在椭圆上(异于点A,B,C)且直线PB,PC分别交直线OA于M,N两点,证明
| OM |
| ON |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)将A,B坐标代入椭圆方程,求出a,b,即可求椭圆的标准方程;
(2)设点C(m,n)(m<0,n<0),则BC中点为(
,
),求得直线OA的方程,利用点C在椭圆上,即可求点C的坐标;
(3)求出M,N的纵坐标,利用点C在椭圆上,结合向量的数量积公式,即可求得结论.
(2)设点C(m,n)(m<0,n<0),则BC中点为(
| m-3 |
| 2 |
| n-3 |
| 2 |
(3)求出M,N的纵坐标,利用点C在椭圆上,结合向量的数量积公式,即可求得结论.
解答:
(1)解:由已知,得
,解得
…(2分)
∴椭圆的标准方程为
+
=1. …(3分)
(2)解:设点C(m,n)(m<0,n<0),则BC中点为(
,
).
由已知,求得直线OA的方程为x-2y=0,从而m=2n-3.①
又∵点C在椭圆上,∴m2+2n2=27.②
由①②,解得n=3(舍),n=-1,从而m=-5. …(5分)
∴点C的坐标为(-5,-1). …(6分)
(3)证明:设P(x0,y0),M(2y1,y1),N(2y2,y2).
∵P,B,M三点共线,∴
=
,整理,得y1=
.…(8分)
∵P,C,N三点共线,∴
=
,整理,得y2=
.…(10分)
∵点C在椭圆上,∴x02+2y02=27,∴x02=27-2y02.
从而y1y2=
=3×
=
. …(14分)
∴
•
=5y1y2=
. …(15分)
∴
•
为定值,定值为
. …(16分)
|
|
∴椭圆的标准方程为
| x2 |
| 27 |
| y2 | ||
|
(2)解:设点C(m,n)(m<0,n<0),则BC中点为(
| m-3 |
| 2 |
| n-3 |
| 2 |
由已知,求得直线OA的方程为x-2y=0,从而m=2n-3.①
又∵点C在椭圆上,∴m2+2n2=27.②
由①②,解得n=3(舍),n=-1,从而m=-5. …(5分)
∴点C的坐标为(-5,-1). …(6分)
(3)证明:设P(x0,y0),M(2y1,y1),N(2y2,y2).
∵P,B,M三点共线,∴
| y1+3 |
| 2y1+3 |
| y0+3 |
| x0+3 |
| 3(y0-x0) |
| x0-2y0-3 |
∵P,C,N三点共线,∴
| y2+1 |
| 2y2+5 |
| y0+1 |
| x0+5 |
| 5y0-x0 |
| x0-2y0+3 |
∵点C在椭圆上,∴x02+2y02=27,∴x02=27-2y02.
从而y1y2=
| 3(3y02-6x0y0+27) |
| 2y02-4x0y0+18 |
| 3 |
| 2 |
| 9 |
| 2 |
∴
| OM |
| ON |
| 45 |
| 2 |
∴
| OM |
| ON |
| 45 |
| 2 |
点评:本题考查椭圆的方程,考查向量的数量积公式,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
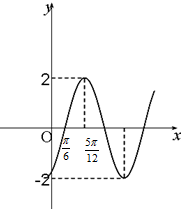 函数f(x)=2sin(ωx+φ),(ω>0,-
函数f(x)=2sin(ωx+φ),(ω>0,-| π |
| 2 |
| π |
| 2 |
A、向右平移
| ||||
B、向右平移
| ||||
C、向右平移
| ||||
D、向右平移
|