题目内容
已知{1，2}⊆M⊆{1，2，3，4，5}，求集合M．
考点：集合的包含关系判断及应用
专题：集合
分析：本题是一道集合包含关系的题目，需要认清集合M的元素，是一道基础题目
解答：
解：∵{1，2}⊆M⊆{1，2，3，4，5}，
∴M集合M中必含有元素1，2，
∴M={1，2}，或M={1，2，3}，或M={1，2，4}，或M={1，2，5}，
或M={1，2，3，4}，或M={1，2，3，5}，或M={1，2，4，5}，或M={1，2，3，4，5}．
∴M集合M中必含有元素1，2，
∴M={1，2}，或M={1，2，3}，或M={1，2，4}，或M={1，2，5}，
或M={1，2，3，4}，或M={1，2，3，5}，或M={1，2，4，5}，或M={1，2，3，4，5}．
点评：本题主要考查集合的包含基本运算，属于基础题．要正确判断两个集合间的关系，必须对集合的相关概念有深刻的理解，善于抓住代表元素，认清集合的特征．
练习册系列答案
相关题目
C是以原点O为中心，焦点在y轴上的等轴双曲线在第一象限部分，曲线C在点P处的切线分别交该双曲线的两条渐近线于A，B两点，则（ ）
A、|OP|＜
| ||
| B、|OP|=|AB| | ||
C、
| ||
D、|OP|=
|
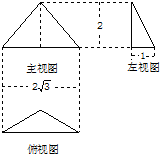已知一个三棱锥的三视图如图所示，其中俯视图是等腰三角形，则该三棱锥的体积为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
已知
=（1，-1），
=（λ，1），
与
的夹角为钝角，则λ的取值范围是（ ）
| a |
| b |
| a |
| b |
| A、λ＞1 |
| B、λ＜1 |
| C、λ＜-1 |
| D、λ＜-1或-1＜λ＜1 |
某几何体的三视图如图所示，则该几何体的体积为（ ）
| A、8π+16 | B、8π-16 |
| C、8π+8 | D、16π-8 |
在直三棱柱中，AA1=AB=BC=3，AC=2，D是AC的中点．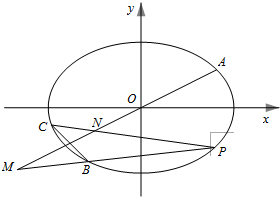
如图，在平面直角坐标系xOy中，已知A，B，C是椭圆