题目内容
把曲线C:y=sin(
-x)•cos(x+
)的图象向右平移a(a>0)个单位,得到曲线C′的图象,且曲线C′的图象关于直线x=
对称,当x∈[
π,
π](b为正整数)时,过曲线C′上任意两点的斜率恒大于零,则b的值为( )
| 7π |
| 8 |
| π |
| 8 |
| π |
| 4 |
| 2b+1 |
| 8 |
| 3b+2 |
| 8 |
| A、1 | B、2 | C、3 | D、4 |
考点:函数y=Asin(ωx+φ)的图象变换,利用导数研究曲线上某点切线方程
专题:三角函数的图像与性质
分析:化简曲线C的解析式为y=
sin(2x+
),可得曲线C′的解析式,再根据图象曲线C′的关于直线x=
对称,求得a=
,故曲线C′的解析式为 y=
sin2x.由题意可得,[
π,
π]是y=
sin2x的一个增区间,而函数 y=
sin2x的增区间为[kπ-
,kπ+
],k∈z,由此求得正整数b的值.
| 1 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 8 |
| 1 |
| 2 |
| 2b+1 |
| 8 |
| 3b+2 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 4 |
| π |
| 4 |
解答:
解:曲线C:y=sin(
-x)•cos(x+
)=sin(x+
)cos(x+
)=
sin(2x+
),
把它的图象向右平移a(a>0)个单位,得到y=
sin[2(x-a)+
]=
sin(2x-2a+
)的图象,
故曲线C′的解析式为 y=
sin(2x-2a+
).
再根据图象曲线C′的关于直线x=
对称,可得 2×
-2a+
=kπ+
,k∈z.
故可取a=
,故曲线C′的解析式为 y=
sin2x.
由题意可得,[
π,
π]是y=
sin2x的一个增区间,
而由2kπ-
≤2x≤2kπ+
,k∈z,求得kπ-
≤x≤kπ+
,k∈z,
故函数 y=
sin2x的增区间为[kπ-
,kπ+
],k∈z.
∴kπ-
≤
π,且
π≤kπ+
,k∈z.
再根据b为正整数,可得b=1,
故选:A.
| 7π |
| 8 |
| π |
| 8 |
| π |
| 8 |
| π |
| 8 |
| 1 |
| 2 |
| π |
| 4 |
把它的图象向右平移a(a>0)个单位,得到y=
| 1 |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 4 |
故曲线C′的解析式为 y=
| 1 |
| 2 |
| π |
| 4 |
再根据图象曲线C′的关于直线x=
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
故可取a=
| π |
| 8 |
| 1 |
| 2 |
由题意可得,[
| 2b+1 |
| 8 |
| 3b+2 |
| 8 |
| 1 |
| 2 |
而由2kπ-
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
故函数 y=
| 1 |
| 2 |
| π |
| 4 |
| π |
| 4 |
∴kπ-
| π |
| 4 |
| 2b+1 |
| 8 |
| 3b+2 |
| 8 |
| π |
| 4 |
再根据b为正整数,可得b=1,
故选:A.
点评:本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性、单调性,属于中档题.

练习册系列答案
相关题目
如图是一个体积为10的空间几何体的三视图,则图中x的值为( )


| A、2 | B、3 | C、4 | D、5 |
设Sn为等差数列{an}的前n项和.若a4<0,a5>|a4|,则使Sn>0成立的最小正整数n为( )
| A、6 | B、7 | C、8 | D、9 |
已知数列{an}是等比数列,且an>0,若bn=log2an,则( )
| A、{bn}一定是递增的等差数列 |
| B、{bn}不可能是等比数列 |
| C、{2b2n-1+1}是等差数列 |
| D、{3bn}不是等比数列 |
若函数f(x)=x+
(b∈R)的导函数在区间(1,2)上有零点,则f(x)在下列区间单调递增的是( )
| b |
| x |
| A、(-2,0) |
| B、(0,1) |
| C、(1,+∞) |
| D、(-∞,-2) |
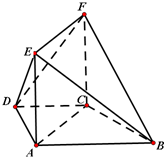 如图,在梯形ABCD中,AB∥CD,∠ABC=60°,AD=CD=CB=a,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a.
如图,在梯形ABCD中,AB∥CD,∠ABC=60°,AD=CD=CB=a,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a.