题目内容
在△ABC中,已知|BC|=2,且
=
,求点A的轨迹方程,并说明轨迹是什么图形.
| |AB| |
| |AC| |
| 2 |
考点:轨迹方程
专题:计算题,直线与圆
分析:以直线BC为x轴、线段BC的中点为原点,建立平面直角坐标系.设点A的坐标为(x,y),由|BC|=2,且
=
,建立方程,化简可得结论.
| |AB| |
| |AC| |
| 2 |
解答:
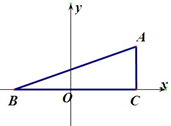 解:如图,以直线BC为x轴、线段BC的中点为原点,建立平面直角坐标系.则有B(-1,0),C(1,0),设点A的坐标为(x,y).-------(2分)
解:如图,以直线BC为x轴、线段BC的中点为原点,建立平面直角坐标系.则有B(-1,0),C(1,0),设点A的坐标为(x,y).-------(2分)
由|BC|=2,且
=
,得
=2
.--(6分)
方程两边同时平方得:(x+1)2+y2=2[(x-1)2+y2],
整理得:x2+y2-6x+1=0.
化成标准方程为:(x-3)2+y2=8-----------------------(10分)
所以,点A的轨迹是以(3,0)为圆心,2
为半径的圆(除去圆与B、C的交点).---(12分)
 解:如图,以直线BC为x轴、线段BC的中点为原点,建立平面直角坐标系.则有B(-1,0),C(1,0),设点A的坐标为(x,y).-------(2分)
解:如图,以直线BC为x轴、线段BC的中点为原点,建立平面直角坐标系.则有B(-1,0),C(1,0),设点A的坐标为(x,y).-------(2分)由|BC|=2,且
| |AB| |
| |AC| |
| 2 |
| (x+1)2+y2 |
| (x-1)2+y2 |
方程两边同时平方得:(x+1)2+y2=2[(x-1)2+y2],
整理得:x2+y2-6x+1=0.
化成标准方程为:(x-3)2+y2=8-----------------------(10分)
所以,点A的轨迹是以(3,0)为圆心,2
| 2 |
点评:本题考查轨迹方程,考查学生的计算能力,正确建立平面直角坐标系是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
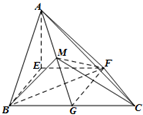 在直角梯形EFCB中,EF∥BC,EF=BE=
在直角梯形EFCB中,EF∥BC,EF=BE=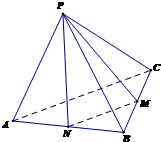 (文科)如图,正四面体P-ABC中,M为线段BC的中点,求异面直线PM与AC所成的角(结果用反三角函数值表示).
(文科)如图,正四面体P-ABC中,M为线段BC的中点,求异面直线PM与AC所成的角(结果用反三角函数值表示).