题目内容
已知数列{an}是等比数列,且an>0,若bn=log2an,则( )
| A、{bn}一定是递增的等差数列 |
| B、{bn}不可能是等比数列 |
| C、{2b2n-1+1}是等差数列 |
| D、{3bn}不是等比数列 |
考点:等比数列的性质
专题:等差数列与等比数列
分析:设正项等比数列{ an }的公比为q(q>0),由若bn=log2an,得数列{bn}是以log2a1为首项,以log2q为公差的等差数列,再根据等差数列与等比数列的定义依次判断,可得答案.
解答:
解:设正项等比数列{ an }的公比为q(q>0),
则an=a1qn-1.
∴bn=log2 an=log2a1+(n-1)log2q.
∴数列{bn}是以log2a1为首项,以log2q为公差的等差数列.
∵当0<q<1时,公差log2q<0,是递减数列,∴A错误;
∵当q=1时,公差为0,数列为常数列,此时数列{bn}也是等比数列,∴B错误;
根据等差数列的性质,数列{bn}是等差数列,则{b2n-1}是等差数列,{2b2n-1+1}是等差数列,故C正确.
∵数列{bn}是等差数列,
∴
=3bn+1-bn=3log2q为常数,∴{3bn}是等比数列,故D错误.
故选C.
则an=a1qn-1.
∴bn=log2 an=log2a1+(n-1)log2q.
∴数列{bn}是以log2a1为首项,以log2q为公差的等差数列.
∵当0<q<1时,公差log2q<0,是递减数列,∴A错误;
∵当q=1时,公差为0,数列为常数列,此时数列{bn}也是等比数列,∴B错误;
根据等差数列的性质,数列{bn}是等差数列,则{b2n-1}是等差数列,{2b2n-1+1}是等差数列,故C正确.
∵数列{bn}是等差数列,
∴
| 3bn+1 |
| 3bn |
故选C.
点评:本题考查了等差、等比数列的判断及等差数列的性质,判断数列{bn}是以log2a1为首项,以log2q为公差的等差数列是解答本题的突破口.

练习册系列答案
相关题目
设
、
、
为平面向量,下面的命题中:
①
•(
-
)=
•
-
•
;
②(
•
)•
=
•(
•
);
③(
-
)2=|
|2-2|
|•|
|+|
|2;
④若
•
=0,则
=
或
=
.
正确的个数是( )
| a |
| b |
| c |
①
| a |
| b |
| c |
| a |
| b |
| a |
| c |
②(
| a |
| b |
| c |
| a |
| b |
| c |
③(
| a |
| b |
| a |
| a |
| b |
| b |
④若
| a |
| b |
| a |
| 0 |
| b |
| 0 |
正确的个数是( )
| A、3 | B、2 | C、1 | D、0 |
在△ABC中,tanB=-2,tanC=
,则A等于( )
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图是一个几何体的三视图,若它的体积为2,则a+b的最小值为
如图是一个几何体的三视图,若它的体积为2,则a+b的最小值为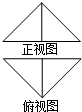 把边长为
把边长为 如图,四面体ABCD中,点A在平面BCD上的射影O在BD上,点M、N分别是BC、BD的中点,AM与平面BCD成45°角,BC⊥CD,∠BDC=30°,BC=2,BO=1
如图,四面体ABCD中,点A在平面BCD上的射影O在BD上,点M、N分别是BC、BD的中点,AM与平面BCD成45°角,BC⊥CD,∠BDC=30°,BC=2,BO=1