题目内容
设Sn为等差数列{an}的前n项和．若a4＜0，a5＞|a4|，则使Sn＞0成立的最小正整数n为（ ）
| A、6 | B、7 | C、8 | D、9 |
考点：等差数列的通项公式
专题：等差数列与等比数列
分析：根据给出的已知条件，得到a5+a4＞0，然后由等差数列的前n项和公式，结合等差数列的性质得答案．
解答：
解：在等差数列{an}中，
∵a4＜0，a5＞|a4|，得
a5＞0，a5+a4＞0，
S7=
=7a4＜0，
S8=
=
=4(a4+a5)＞0．
∴使Sn＞0成立的最小正整数n为8．
故选：C．
∵a4＜0，a5＞|a4|，得
a5＞0，a5+a4＞0，
S7=
| 7(a1+a7) |
| 2 |
S8=
| 8(a1+a8) |
| 2 |
| 8(a4+a5) |
| 2 |
∴使Sn＞0成立的最小正整数n为8．
故选：C．
点评：本题考查等差数列的通项公式，考查了等差数列的性质，是基础题．
练习册系列答案
新黄冈兵法密卷系列答案
相关题目
若关于x的方程|2x-1|=m有两个不相等的实数根x1和x2，则有（ ）
| A、x1+x2＞0 |
| B、x1+x2≥0 |
| C、x1+x2≤0 |
| D、x1+x2＜0 |
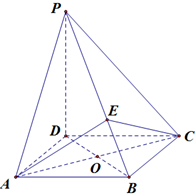如图，四棱锥P-ABCD的底面是正方形，PD⊥底面ABCD，AC，BD相交于点O，