题目内容
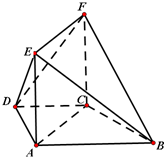 如图,在梯形ABCD中,AB∥CD,∠ABC=60°,AD=CD=CB=a,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a.
如图,在梯形ABCD中,AB∥CD,∠ABC=60°,AD=CD=CB=a,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a.(Ⅰ)求证:BC⊥平面ACFE;
(Ⅱ)求二面角B-EF-D的余弦值.
考点:与二面角有关的立体几何综合题,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(Ⅰ)由已知条件推导出四边形ABCD是等腰梯形,进而推导出AC⊥BC,由此能证明BC⊥平面ACFE.
(Ⅱ)取EF中点G,EB中点H,连结DG、GH、DH,由题设条件推导出∠DGH是二面角B-EF-D的平面角,由此能求出二面角B-EF-D的平面角余弦值.
(Ⅱ)取EF中点G,EB中点H,连结DG、GH、DH,由题设条件推导出∠DGH是二面角B-EF-D的平面角,由此能求出二面角B-EF-D的平面角余弦值.
解答:
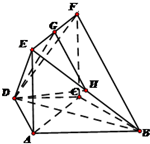 解:(Ⅰ)在梯形ABCD中,AB∥CD,
解:(Ⅰ)在梯形ABCD中,AB∥CD,
∵∠ABC=60°,AD=CD=CB=a,
∴四边形ABCD是等腰梯形,…(2分)
且∠DCA=∠DAC=30°,∠DCB=120°,
∴∠ACB=∠DCB-∠DCA=90°,
∴AC⊥BC.…(4分)
又∵平面ACFE⊥平面ABCD,交线为AC,
∴BC⊥平面ACFE.…(6分)
(Ⅱ)取EF中点G,EB中点H,连结DG、GH、DH,
∵AD=CD=CB=a,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a.
∴DE=DF,∴DG⊥EF,…(8分)
∵BC⊥平面ACFE,∴BC⊥EF,
又∵EF⊥FC,∴EF⊥FB,
又∵GH∥BF,∴EF⊥GH,
∴∠DGH是二面角B-EF-D的平面角.…(10分)
在△BDE中,DE=
a,DB=
a,BE=
=
a,
∴BE2=DE2+DB2,∴∠EDB=90°,
∴DH=
a,又DG=
a,GH=
a,…(12分)
∴在△DGH中,由余弦定理得
cos∠DGH=
,
∴二面角B-EF-D的平面角余弦值为
.…(14分)
(注:若用空间向量解答,则酌情给分.)
 解:(Ⅰ)在梯形ABCD中,AB∥CD,
解:(Ⅰ)在梯形ABCD中,AB∥CD,∵∠ABC=60°,AD=CD=CB=a,
∴四边形ABCD是等腰梯形,…(2分)
且∠DCA=∠DAC=30°,∠DCB=120°,
∴∠ACB=∠DCB-∠DCA=90°,
∴AC⊥BC.…(4分)
又∵平面ACFE⊥平面ABCD,交线为AC,
∴BC⊥平面ACFE.…(6分)
(Ⅱ)取EF中点G,EB中点H,连结DG、GH、DH,
∵AD=CD=CB=a,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a.
∴DE=DF,∴DG⊥EF,…(8分)
∵BC⊥平面ACFE,∴BC⊥EF,
又∵EF⊥FC,∴EF⊥FB,
又∵GH∥BF,∴EF⊥GH,
∴∠DGH是二面角B-EF-D的平面角.…(10分)
在△BDE中,DE=
| 2 |
| 3 |
| AE2+AB2 |
| 5 |
∴BE2=DE2+DB2,∴∠EDB=90°,
∴DH=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
∴在△DGH中,由余弦定理得
cos∠DGH=
| ||
| 10 |
∴二面角B-EF-D的平面角余弦值为
| ||
| 10 |
(注:若用空间向量解答,则酌情给分.)
点评:本题考查直线与平面垂直的证明,考查二面角的平面角的余弦值的求法,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
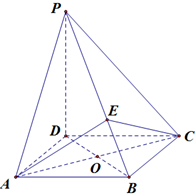 如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,AC,BD相交于点O,
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,AC,BD相交于点O, 如图,四面体ABCD中,点A在平面BCD上的射影O在BD上,点M、N分别是BC、BD的中点,AM与平面BCD成45°角,BC⊥CD,∠BDC=30°,BC=2,BO=1
如图,四面体ABCD中,点A在平面BCD上的射影O在BD上,点M、N分别是BC、BD的中点,AM与平面BCD成45°角,BC⊥CD,∠BDC=30°,BC=2,BO=1 如图,P为线段AB的垂直平分线上任意一点,O为平面内的任意一点,设
如图,P为线段AB的垂直平分线上任意一点,O为平面内的任意一点,设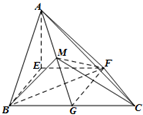 在直角梯形EFCB中,EF∥BC,EF=BE=
在直角梯形EFCB中,EF∥BC,EF=BE=