题目内容
若函数f(x)=x+
(b∈R)的导函数在区间（1，2）上有零点，则f（x）在下列区间单调递增的是（ ）
| b |
| x |
| A、（-2，0） |
| B、（0，1） |
| C、（1，+∞） |
| D、（-∞，-2） |
考点：利用导数研究函数的单调性,函数在某点取得极值的条件
专题：导数的综合应用
分析：本题先根据导函数在区间（1，2）上有零点，得到b的取值范围，再利用b的取值范围，求出函数的单调增区间，结合b的取值范围，选择符合题意的选项．
解答：
解：∵函数f(x)=x+
(b∈R)
∴f ′(x)=1-
∵函数f(x)=x+
(b∈R)的导函数在区间（1，2）上有零点
∴当1-
=0时，b=x2，x∈（1，2）
∴b∈（1，4）
令f'（x）＞0 得到x＜-
或x＞
即f（x）的单调增区间为（-∞，-
），（
，+∞）
∵b∈（1，4）
∴（-∞，-2）适合题意
故选D
| b |
| x |
∴f ′(x)=1-
| b |
| x2 |
∵函数f(x)=x+
| b |
| x |
∴当1-
| b |
| x2 |
∴b∈（1，4）
令f'（x）＞0 得到x＜-
| b |
| b |
即f（x）的单调增区间为（-∞，-
| b |
| b |
∵b∈（1，4）
∴（-∞，-2）适合题意
故选D
点评：本题在研究了b的取值范围后，得到了函数f（x）的单调增区间，在选择选项时，要注意选择恒成立的选项．
练习册系列答案
相关题目
若关于x的方程|2x-1|=m有两个不相等的实数根x1和x2，则有（ ）
| A、x1+x2＞0 |
| B、x1+x2≥0 |
| C、x1+x2≤0 |
| D、x1+x2＜0 |
m是一条直线，α，β是两个不同的平面，以下命题正确的是（ ）
| A、若m∥α，α∥β，则m∥β |
| B、若m∥α，m∥β，则α∥β |
| C、若m∥α，α⊥β，则m⊥β |
| D、若m∥α，m⊥β，则α⊥β |
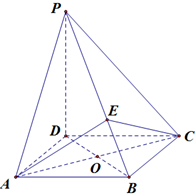如图，四棱锥P-ABCD的底面是正方形，PD⊥底面ABCD，AC，BD相交于点O，
如图，P为线段AB的垂直平分线上任意一点，O为平面内的任意一点，设