题目内容
5根木棒长度分别是2,3,5,7,9,从中任取3根,则取出的3根木棒长度能构成三角形的概率 .
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:由三角形的性质,我们可得三条线段能构成三角形时,必须满足两小边之和大于第三边,我们可以列举出所有事件的个数,及满足条件的事件个数,然后代入古典概型计算公式即可求解.
解答:
解:从五条线段中抽取三条,按边长由小到大的顺序表示为(a,b,c),则共有:
(2,3,5),(2,3,7),(2,3,9),(2,5,7),(2,5,9)
(2,7,9),(3,5,7),(3,5,9),(3,7,9),(5,7,9)共10种
其中能构成三角形的有:
(3,5,7),(3,7,9),(5,7,9)共3种
故从中任取三条,能构成三角形的概率P=0.3;
故答案为:0.3.
(2,3,5),(2,3,7),(2,3,9),(2,5,7),(2,5,9)
(2,7,9),(3,5,7),(3,5,9),(3,7,9),(5,7,9)共10种
其中能构成三角形的有:
(3,5,7),(3,7,9),(5,7,9)共3种
故从中任取三条,能构成三角形的概率P=0.3;
故答案为:0.3.
点评:本题考查了利用列举法求古典概型的概率;正确把握各个事件的相互关系是解决问题的关键.解决问题的步骤是:计算满足条件的基本事件个数,及基本事件的总个数,然后代入古典概型计算公式进行求解.

练习册系列答案
相关题目
在△ABC中,已知a=3,b=4,c=2,则c•cosB+b•cosC=( )
| A、2 | B、3 | C、4 | D、5 |
在下列函数中,同时满足:①在(0,
)上递增;②以2π为周期;③是奇函数的是( )
| π |
| 2 |
| A、y=tanx | ||
| B、y=cosx | ||
C、y=tan
| ||
| D、y=-tanx |
函数y=2sin(
-x),x∈[
,
]的最小值和最大值分别是( )
| π |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
A、-
| ||
| B、-1和2 | ||
| C、1和3 | ||
| D、1和2 |
函数y=ax(a>0且a≠1)在[0,1]上的最大值与最小值的差为
,则a等于( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、
|
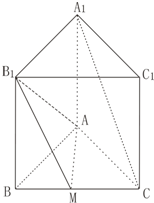 如图正三棱柱ABC-A1B1C1中底面边长AB=1,高BB1=1,M为底面BC边的中点.
如图正三棱柱ABC-A1B1C1中底面边长AB=1,高BB1=1,M为底面BC边的中点.