题目内容
有4位同学，每人买1张体育彩票，则至少有2位同学想所买彩票的末位数相同的概率为 ．
考点：古典概型及其概率计算公式
专题：概率与统计
分析：先计算每位同学彩票号码的末位数字各不相同的概率，再由对立事件概率计算公式求至少有两位同学彩票号码的末位数字相同的概率．
解答：
解：假设每位同学都是随机选号，彩票号码的末位数字是0-9的概率均等，
每位同学彩票号码的末位数字都有10种可能，共有104=10000种组合，
计算每位同学彩票号码的末位数字各不相同的概率：
第一位同学有彩票号码的末位数字有10种可能，第二位同学要跟他不同就只有9种，
第三位同学要跟前面两位不同就是8种，第四位同学7种，共有
=10×9×8×7=5040种组合．
∴每位同学彩票号码的末位数字各不相同的概率P1=
=0.504，
∴至少有两位同学彩票号码的末位数字相同的概率 P=1-0.504=0.496．
故答案为：0.496．
每位同学彩票号码的末位数字都有10种可能，共有104=10000种组合，
计算每位同学彩票号码的末位数字各不相同的概率：
第一位同学有彩票号码的末位数字有10种可能，第二位同学要跟他不同就只有9种，
第三位同学要跟前面两位不同就是8种，第四位同学7种，共有
| A | 4 10 |
∴每位同学彩票号码的末位数字各不相同的概率P1=
| 5040 |
| 10000 |
∴至少有两位同学彩票号码的末位数字相同的概率 P=1-0.504=0.496．
故答案为：0.496．
点评：本题考查概率的求法，是基础题，解题时要认真审题，注意对立事件概率计算公式的合理运用．
练习册系列答案
名校课堂系列答案
相关题目
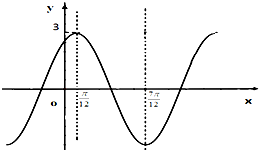已知函数f（x）=Asin（wx+φ）（w＞0，A＞0，|φ|＜
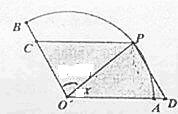半径为1，圆心角为120°的扇形，点P是扇形AB弧上的动点，设∠POA=x．