题目内容
若函数f（x）=
-lnx在区间（2，+∞）上单调递减，则实数k的取值范围是 ．
| k |
| x |
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：由题意可知在区间（2，+∞）上f′（x）=-
-
≤0恒成立，即在x∈（2，+∞）上x+k≥0，所以k≥-2．
| k |
| x2 |
| 1 |
| x |
解答：
解：∵f（x）=
-lnx，
∴f′（x）=-
-
=-
，
∵数f（x）=
-lnx在区间（2，+∞）上单调递减，
∴f′（x）=-
≤0在x∈（2，+∞）上恒成立，
即，在x∈（2，+∞）上，x+k≥0，
∴2+k≥0
∴k≥-2．
故答案为k≥-2
| k |
| x |
∴f′（x）=-
| k |
| x2 |
| 1 |
| x |
| x+k |
| x2 |
∵数f（x）=
| k |
| x |
∴f′（x）=-
| x+k |
| x2 |
即，在x∈（2，+∞）上，x+k≥0，
∴2+k≥0
∴k≥-2．
故答案为k≥-2
点评：本题主要考查利用导数研究函数的单调性，函数的单调性的性质，属于基础题．
练习册系列答案
相关题目
以下命题：
①在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么它和这条斜线垂直；
②已知平面α，β的法向量分别为
，
，则α⊥β?
•
=0；
③两条异面直线所成的角为θ，则0≤θ≤
；
④直线与平面所成的角为φ，则0≤φ≤
．
其中正确的命题是（ ）
①在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么它和这条斜线垂直；
②已知平面α，β的法向量分别为
| u |
| v |
| u |
| v |
③两条异面直线所成的角为θ，则0≤θ≤
| π |
| 2 |
④直线与平面所成的角为φ，则0≤φ≤
| π |
| 2 |
其中正确的命题是（ ）
| A、①②③ | B、②③④ |
| C、①②④ | D、①③④ |
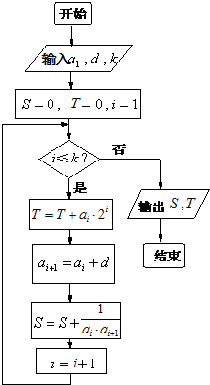如图所示，程序框图给出了无穷正项数列{an}满足的条件，且当k=5时，输出的S是
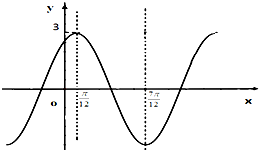已知函数f（x）=Asin（wx+φ）（w＞0，A＞0，|φ|＜已知函数g（x）=ax+a，f（x）=
，若对任意的x1∈[-2，2]，存在x2∈[-2，2]，使g（x1）=f（x2）成立，则a的取值范围是（ ）
|
A、[-
| ||
B、[-
| ||
| C、（0，1] | ||
| D、（-∞，1] |