题目内容
已知圆C1:x2+y2=1与圆C2:(x-3)2+(x-4)2=a(a>0)外切,则a= .
考点:圆与圆的位置关系及其判定
专题:直线与圆
分析:求出两个圆的圆心与半径,从而得到它们的圆心间的距离等于半径和,列出方程即可求出a.
解答:
解:∵圆C1:x2+y2=1与圆C2:(x-3)2+(x-4)2=a(a>0)的圆心分别为(0,O),(3,4);半径分别为r1=1,r2=
,
∴两圆的圆心间的距离等于d=
=5,而半径和为:1+
.
∴1+
=5,
解得a=16.
故答案为:16.
| a |
∴两圆的圆心间的距离等于d=
| 32+42 |
| a |
∴1+
| a |
解得a=16.
故答案为:16.
点评:本题给出两圆的方程,通过它们的相切关系列出方程的解题的关键.着重考查了圆的标准方程、圆与圆的位置关系等知识,属于中档题.

练习册系列答案
相关题目
以下命题:
①在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它和这条斜线垂直;
②已知平面α,β的法向量分别为
,
,则α⊥β?
•
=0;
③两条异面直线所成的角为θ,则0≤θ≤
;
④直线与平面所成的角为φ,则0≤φ≤
.
其中正确的命题是( )
①在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它和这条斜线垂直;
②已知平面α,β的法向量分别为
| u |
| v |
| u |
| v |
③两条异面直线所成的角为θ,则0≤θ≤
| π |
| 2 |
④直线与平面所成的角为φ,则0≤φ≤
| π |
| 2 |
其中正确的命题是( )
| A、①②③ | B、②③④ |
| C、①②④ | D、①③④ |
已知函数g(x)=ax+a,f(x)=
,若对任意的x1∈[-2,2],存在x2∈[-2,2],使g(x1)=f(x2)成立,则a的取值范围是( )
|
A、[-
| ||
B、[-
| ||
| C、(0,1] | ||
| D、(-∞,1] |
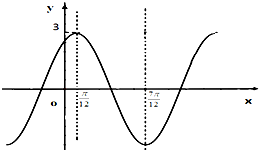 已知函数f(x)=Asin(wx+φ)(w>0,A>0,|φ|<
已知函数f(x)=Asin(wx+φ)(w>0,A>0,|φ|<