题目内容
已知四面体P-ABC的四个顶点都在球O的球面上,若PB⊥平面ABC,AB⊥AC,且AC=1,PB=AB=2,则球O的体积为( )
A、
| ||
B、
| ||
| C、4π | ||
D、
|
考点:球的体积和表面积
专题:计算题,空间位置关系与距离,球
分析:根据条件,根据四面体P-ABC构造长方体,然后根据长方体和球的直径之间的关系,即可求出球的半径,再求球的体积公式计算即可得到.
解答:
解:∵PB⊥平面ABC,AB⊥AC,且AC=1,PB=AB=2,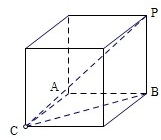
∴构造长方体,则长方体的外接球和四面体的外接球是相同的,
则长方体的体对角线等于球的直径2R,
则2R=
=3,
∴R=
,
则球O的体积为
πR3=
π×(
)3=
π.
故选D.

∴构造长方体,则长方体的外接球和四面体的外接球是相同的,
则长方体的体对角线等于球的直径2R,
则2R=
| 12+22+22 |
∴R=
| 3 |
| 2 |
则球O的体积为
| 4 |
| 3 |
| 4 |
| 3 |
| 3 |
| 2 |
| 9 |
| 2 |
故选D.
点评:本题主要考查空间几何体的位置关系,利用四面体构造长方体是解决本题的关键,利用长方体的体对角线等于球的直径是本题的突破点.

练习册系列答案
相关题目
从区间(-3,3)中任取两个整数a,b,设点(a,b)在圆x2+y2=3内的概率为 P1,从区间(-3,3)中任取两个实数a,b,直线ax+by+3=0和圆x2+y2=3相离的概率为 P2,则( )
| A、P1>P2 |
| B、P1<P2 |
| C、P1=P2 |
| D、P1和 P2的大小关系无法确定 |
已知函数f(x)是定义在R上的奇函数,且对任意x都有f(x+2)=f(x).当x∈[0,1)时,f(x)=2x-1,则f(log
6)的值为( )
| 1 |
| 2 |
A、-
| ||
| B、-5 | ||
C、-
| ||
| D、-6 |
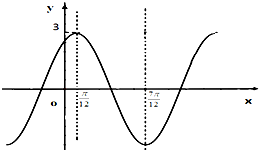 已知函数f(x)=Asin(wx+φ)(w>0,A>0,|φ|<
已知函数f(x)=Asin(wx+φ)(w>0,A>0,|φ|<