题目内容

数列求和、错位相减：bn=（2n-1）（
1
2
）n．
考点：数列的求和
专题：等差数列与等比数列
分析：直接由错位相减法求数列{bn}的前n项和．
解答： 解：由bn=（2n-1）（
1
2
）n，
得Sn=b1+b2+…+bn
=1•
1
2
+3•(
1
2
)2+…+(2n-1)•(
1
2
)n，
1
2
Sn=1•(
1
2
)2+3•(
1
2
)3+…+(2n-3)•(
1
2
)n+(2n-1)•(
1
2
)n+1．
两式作差得：
1
2
Sn=
1
2
+2[(
1
2
)2+(
1
2
)3+…+(
1
2
)n]-(2n-1)•(
1
2
)n+1
=
1
2
+2•
1
4
[1-(
1
2
)n-1]
1-
1
2
-(2n-1)•(
1
2
)n+1=
3
2
-(2n+3)•(
1
2
)n+1．
∴Sn=3-(2n+3)•(
1
2
)n．
点评：本题考查了错位相减法求数列的前n项和，关键注意作差后末项的符号，是中档题．
练习册系列答案
相关题目
从区间（-3，3）中任取两个整数a，b，设点（a，b）在圆x2+y2=3内的概率为 P1，从区间（-3，3）中任取两个实数a，b，直线ax+by+3=0和圆x2+y2=3相离的概率为 P2，则（　　）
A、P1＞P2
B、P1＜P2
C、P1=P2
D、P1和 P2的大小关系无法确定
已知A（x1，y1），B（x2，y2）是f（x）=
1
2
+log2
x
1-x
图象上任意两点，设点M（
1
2
，b）为AB的中点，若Sn=f（
1
n
）+f（
2
n
）+f（
3
n
）+…+f（
n-1
n
），其中n∈N+，则n≥2，求Sn．
在三角形 A BC中，A，B，C是三角形 A BC的内角，设函数f（A）=2sin
B+C
2
sin（π-
A
2
）+sin2（π+
A
2
）-cos2
A
2
，则f（ A）的最大值为
 
．
已知不等式f（x）=|x-2|-|x-1|
（Ⅰ）若f（x）≤m的解集为R，求m的最小值；
（Ⅱ）若f（x）最大值为n且a+b+c=n，求证：a2+b2+c2≥
1
3
．
执行如图所示的程序框图，则输出的a的值为（注：“a=2”，即为“a←2”或为“a：=2”．）（　　）
A、2
B、
1
3
C、-
1
2
D、-3
以下命题：
①在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么它和这条斜线垂直；
②已知平面α，β的法向量分别为
u
，
v
，则α⊥β?
u
•
v
=0；
③两条异面直线所成的角为θ，则0≤θ≤
π
2
；
④直线与平面所成的角为φ，则0≤φ≤
π
2
．
其中正确的命题是（　　）
A、①②③B、②③④
C、①②④D、①③④
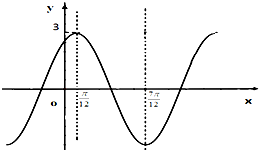已知函数f（x）=Asin（wx+φ）（w＞0，A＞0，|φ|＜
π
2
）的图象如图所示，
（1）求f（x）的解析式；
（2）若f（
θ
2
-
π
6
）=
12
5
，θ∈（0，
π
2
），求cos（θ-
π
3
）的值．
已知点O（0，0），M（1，0），双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的一条渐近线上有一点P，满足|
OP
|=6，
OM
•
OP
=3．
（1）求渐近线方程；
（2）若双曲线C过点（2，3），求双曲线方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网