题目内容
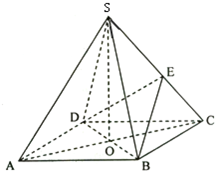 已知如图,在四棱锥S-ABCD中,底面ABCD是菱形,AC与BD的交点为O,SO⊥平面ABCD,E为侧棱SC上一个动点.
已知如图,在四棱锥S-ABCD中,底面ABCD是菱形,AC与BD的交点为O,SO⊥平面ABCD,E为侧棱SC上一个动点.(1)求证:平面SAC⊥平面BDE;
(2)若E为SC的中点,求证:SA∥平面BDE;
(3)若E为SC的中点,AB=SO=a,∠BAD=60°,求三棱锥S-BDE的体积.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)由SA⊥平面ABCD,BD?平面ABCD,知SA⊥BD,由底面ABCD为正方形,知BD⊥AC,由此能够证明面EBD⊥面SAC.
(2)要证明SA∥平面BDE,只需证明SA平行于平面BDE内的一条直线即可,而E为中点,所以连接AC、BD交于点O.由条件知道O为AC中点,从而EO为三角形SAC的中位线,从而得到SA∥OE,得证;
(3)由已知中E为SC的中点,AB=SO=a,∠BAD=60°,先求出三棱锥S-BDC的体积和三棱锥E-BDC的体积,相减可得答案.
(2)要证明SA∥平面BDE,只需证明SA平行于平面BDE内的一条直线即可,而E为中点,所以连接AC、BD交于点O.由条件知道O为AC中点,从而EO为三角形SAC的中位线,从而得到SA∥OE,得证;
(3)由已知中E为SC的中点,AB=SO=a,∠BAD=60°,先求出三棱锥S-BDC的体积和三棱锥E-BDC的体积,相减可得答案.
解答:
证明:(1)∵SA⊥平面ABCD,BD?平面ABCD,
∴SA⊥BD,
∵底面ABCD为正方形,
∴BD⊥AC,
∵SA∩AC=A,
∴BD⊥平面SAC,
∵BD?平面EBD,
∴面EBD⊥面SAC.
(2)连接OE,

∵四边形ABCD是菱形,
∴O为AC的中点,
又∵E为SC的中点,
∴OE为三角形SAC的中位线,
∴SA∥OE,
又∵OE?面BDE,SA?面BDE,
∴SA∥平面BDE;
(3)∵AB=SO=a,∠BAD=60°,
∴S△BCD=
BC•CD•sin60°=
a2,
∴三棱锥S-BDC的体积为:
×
a2×a=
a3,
∵E为SC的中点,
故三棱锥E-BDC的高为:
a,
故三棱锥E-BDC的体积为:
×
a2×
a=
a3,
故三棱锥S-BDE的体积V=
a3-
a3=
a3
∴SA⊥BD,
∵底面ABCD为正方形,
∴BD⊥AC,
∵SA∩AC=A,
∴BD⊥平面SAC,
∵BD?平面EBD,
∴面EBD⊥面SAC.
(2)连接OE,

∵四边形ABCD是菱形,
∴O为AC的中点,
又∵E为SC的中点,
∴OE为三角形SAC的中位线,
∴SA∥OE,
又∵OE?面BDE,SA?面BDE,
∴SA∥平面BDE;
(3)∵AB=SO=a,∠BAD=60°,
∴S△BCD=
| 1 |
| 2 |
| ||
| 4 |
∴三棱锥S-BDC的体积为:
| 1 |
| 3 |
| ||
| 4 |
| ||
| 12 |
∵E为SC的中点,
故三棱锥E-BDC的高为:
| 1 |
| 2 |
故三棱锥E-BDC的体积为:
| 1 |
| 3 |
| ||
| 4 |
| 1 |
| 2 |
| ||
| 24 |
故三棱锥S-BDE的体积V=
| ||
| 12 |
| ||
| 24 |
| ||
| 24 |
点评:本题考查平面与平面垂直的证明,考查直线与平面平行的证明,考查棱锥的体积的求法,解题时要认真审题,仔细解答,难度中档.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
设集合M={x|x≥-1},N={x|x≤k},若M∩N≠¢,则k的取值范围是( )
| A、(-∞,-1] |
| B、[-1,+∞) |
| C、(-1,+∞) |
| D、(-∞,-1) |
已知函数f(x)=
,若关于x的方程f[f(x)]=0有且仅有一解,则实数a的取值范围是( )
|
| A、(-∞,0) |
| B、(-∞,0)∪(0,1) |
| C、(0,1) |
| D、(0,1)∪(1,+∞) |