题目内容
已知函数f(x)=
,若关于x的方程f[f(x)]=0有且仅有一解,则实数a的取值范围是( )
|
| A、(-∞,0) |
| B、(-∞,0)∪(0,1) |
| C、(0,1) |
| D、(0,1)∪(1,+∞) |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:分a=0、a>0、a<0三种情况讨论.
利用换元法设t=f(x),则方程等价为f(t)=0,作出函数f(x)的图象,利用数形结合即可得出.
利用换元法设t=f(x),则方程等价为f(t)=0,作出函数f(x)的图象,利用数形结合即可得出.
解答:
解:(1)当a=0时,在x≤0的条件下,f(x)=0,此时方程f[f(x)]=0有无数解,不符合题意;
(2)当a>0时,画此分段函数的图象:
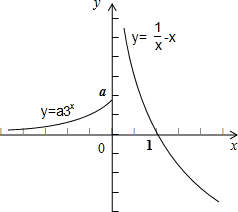
设t=f(x),则f(t)=0,
c从图象上看,f(t)=0有唯一解,t=1,则f(x)=1,
要使方程有唯一解,∴a<1.
∴0<a<1
(3)当a<0时,画此分段函数的图象:
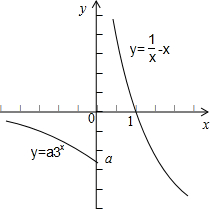
设t=f(x),则f(t)=0,
c从图象上看,f(t)=0有唯一解,t=1,则f(x)=1,
要使方程有唯一解,再从图象上看不管a取何值,f(x)=1只有一解,
∴a<0
综上(1)(2)(3):实数a的取值范围是(-∞,0)∪(0,1),
故选:B
(2)当a>0时,画此分段函数的图象:
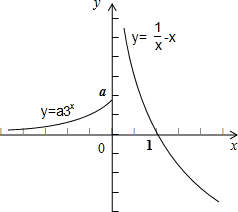
设t=f(x),则f(t)=0,
c从图象上看,f(t)=0有唯一解,t=1,则f(x)=1,
要使方程有唯一解,∴a<1.
∴0<a<1
(3)当a<0时,画此分段函数的图象:
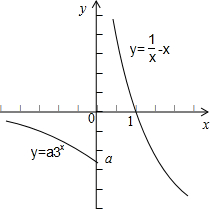
设t=f(x),则f(t)=0,
c从图象上看,f(t)=0有唯一解,t=1,则f(x)=1,
要使方程有唯一解,再从图象上看不管a取何值,f(x)=1只有一解,
∴a<0
综上(1)(2)(3):实数a的取值范围是(-∞,0)∪(0,1),
故选:B
点评:本题主要考查函数方程根的个数的应用,利用换元法,结合数形结合是解决本题的关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
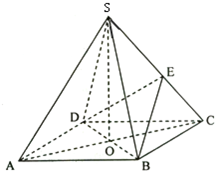 已知如图,在四棱锥S-ABCD中,底面ABCD是菱形,AC与BD的交点为O,SO⊥平面ABCD,E为侧棱SC上一个动点.
已知如图,在四棱锥S-ABCD中,底面ABCD是菱形,AC与BD的交点为O,SO⊥平面ABCD,E为侧棱SC上一个动点.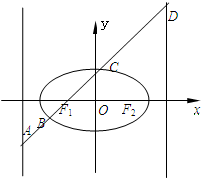 如图,已知椭圆
如图,已知椭圆