题目内容
已知A={x|x2-3x+4=0},B={x∈R|(x+1)(x2+3x-4)=0},求满足条件A?P⊆B的集合P.
考点:集合的包含关系判断及应用
专题:集合
分析:求出方程x2-3x+4=0的判别式△后即求出A,再求出(x+1)(x2+3x-4)=0的根即求出B,再由条件列出集合B的非空子集即为集合P.
解答:
解:由于方程x2-3x+4=0的判别式△=9-16=-7<0,知A=∅,
由(x+1)(x2+3x-4)=0得,x+1=0或x2+3x-4=0,解得x=-1或1或-4,则B={-1,1,-4},
∵A?P⊆B,∴集合P≠∅,且其元素全属于B,即集合P为集合B的非空子集:
{1}或{-1}或{-4}或{-1,1}或{-1,-4}或{1,-4}或{-1,1,-4}.
由(x+1)(x2+3x-4)=0得,x+1=0或x2+3x-4=0,解得x=-1或1或-4,则B={-1,1,-4},
∵A?P⊆B,∴集合P≠∅,且其元素全属于B,即集合P为集合B的非空子集:
{1}或{-1}或{-4}或{-1,1}或{-1,-4}或{1,-4}或{-1,1,-4}.
点评:本题考查了集合间的包含关系和列举法求已知集合的子集,解题的关键:必须确定满足条件的集合P的元素,即明确A、B,充分把握子集、真子集的概念,准确化简集合是解决问题的首要条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知集合A={x∈Z|x2-1≤0},B={x|x2-x-2=0},则A∩B=( )
| A、∅ | B、{-1} |
| C、{0} | D、{2} |
函数f(x)=
+
的定义域是( )
| x+3 |
| (2x+3)0 | ||
|
A、[-3,
| ||||||
B、[-3,-
| ||||||
C、[-3,
| ||||||
D、[-3,-
|
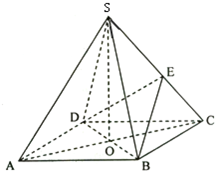 已知如图,在四棱锥S-ABCD中,底面ABCD是菱形,AC与BD的交点为O,SO⊥平面ABCD,E为侧棱SC上一个动点.
已知如图,在四棱锥S-ABCD中,底面ABCD是菱形,AC与BD的交点为O,SO⊥平面ABCD,E为侧棱SC上一个动点.