题目内容
已知函数y=loga(x+3)+
(a>0,a≠1)的图象恒过定点A,若点A也在函数f(x)=3x+b的图象上,则 b= .
| 8 |
| 9 |
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:先利用函数y=loga(x+3)+
的解析式得出其图象必过哪一个定点,再将该定点的坐标代入函数函数f(x)=3x+b式中求出b,问题得以解决.
| 8 |
| 9 |
解答:
解:∵令x+3=1,即x=-2,则y=
,
∴函数y=loga(x+3)+
(a>0,a≠1)的图象恒过定点A(-2,
),
将x=-2,y=
代入y=3x+b得:3-2+b=
,∴b=
,
故答案为:
| 8 |
| 9 |
∴函数y=loga(x+3)+
| 8 |
| 9 |
| 8 |
| 9 |
将x=-2,y=
| 8 |
| 9 |
| 8 |
| 9 |
| 7 |
| 9 |
故答案为:
| 7 |
| 9 |
点评:本题考查对数函数、指数函数的图象的图象与性质,考查数形结合的数学思想,属于基础题.

练习册系列答案
相关题目
已知集合A={x∈Z|x2-1≤0},B={x|x2-x-2=0},则A∩B=( )
| A、∅ | B、{-1} |
| C、{0} | D、{2} |
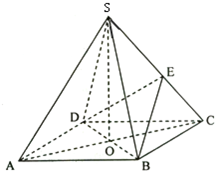 已知如图,在四棱锥S-ABCD中,底面ABCD是菱形,AC与BD的交点为O,SO⊥平面ABCD,E为侧棱SC上一个动点.
已知如图,在四棱锥S-ABCD中,底面ABCD是菱形,AC与BD的交点为O,SO⊥平面ABCD,E为侧棱SC上一个动点.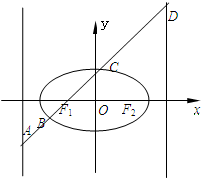 如图,已知椭圆
如图,已知椭圆
 △ABC中,AB=4,AC=4
△ABC中,AB=4,AC=4